summary

모든 노드가 동일한 degree를 갖는 그래프, degree matrix가 \(I\)나 \(kI\)로 나타낼 수 있는 그래프

degree matrix: the degree matrix of an undirected graph is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex.

Import

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

Regular Graph

definition of wiki: each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency.

모든 node가 동일한 degree를 갖는 그래프

Tip

Tip for future work

이것은 시계열에서의 Graph Shift Operator로써 볼 수 있지.¹

¹ 단, 단위행렬일때, 단위행렬의 배수가 아니라.

w=np.zeros((5,5))
for i in range(5):
    for j in range(5):
        if i==j :
            w[i,j] = 0
        elif i-j == 1 : 
            w[i,j] = 1
        elif j-i == 4 :
            w[i,j] = 1

array([[0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.]])

lst = []
for i in range(5):
    for j in range(5):
        if w[i,j] == 1:
            lst.append([i,j])

np.array(lst)

array([[0, 4],
       [1, 0],
       [2, 1],
       [3, 2],
       [4, 3]])

동일한 차수를 갖는다?

Note

참고로, 무조건 degree matrix가 단위행렬일 필요는 없고 \(D = kI\)가 성립해도 Regular Graph

d= w.sum(axis=1)
D= np.diag(d)

array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)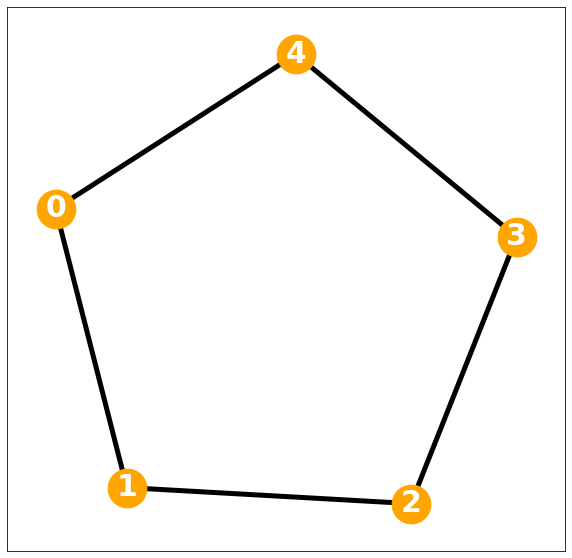

Non-Regular Graph

w = np.array([[0., 0., 0., 0., 0.],
       [1., 0., 1., 1., 1.],
       [1., 1., 0., 0., 1.],
       [0., 0., 1., 0., 1.],
       [0., 0., 0., 0., 0.]])

lst = []
for i in range(5):
    for j in range(5):
        if w[i,j] == 1:
            lst.append([i,j])

np.array(lst)

array([[1, 0],
       [1, 2],
       [1, 3],
       [1, 4],
       [2, 0],
       [2, 1],
       [2, 4],
       [3, 2],
       [3, 4]])

Note

모든 Degree가 동일하는 가정이 무너져 regular graph 로 정의할 수 없음

d= w.sum(axis=1)
D= np.diag(d)

array([[0., 0., 0., 0., 0.],
       [0., 4., 0., 0., 0.],
       [0., 0., 3., 0., 0.],
       [0., 0., 0., 2., 0.],
       [0., 0., 0., 0., 0.]])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)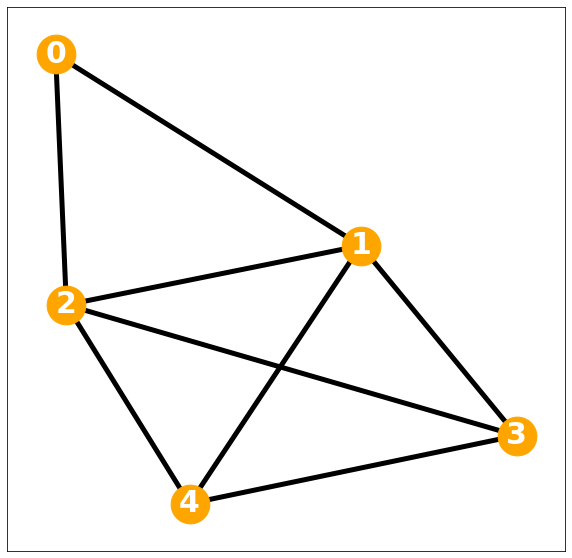

Several Types of regular graph

0-regular graph

참고 아래도 동일 차수이므로 regular graph

w = np.array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

d= w.sum(axis=1)
D= np.diag(d)

Degree matrix = \(I\)

array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

lst = []
for i in range(5):
    for j in range(5):
        if w[i,j] == 1:
            lst.append([i,j])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)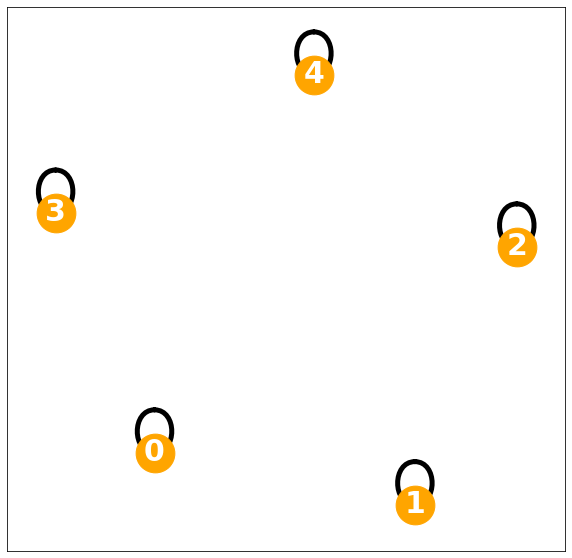

1-regular graph

w = np.array([
       [0., 1., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0.],
       [0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 0., 0., 1.],
       [0., 0., 0., 0., 1., 0.]])

d= w.sum(axis=1)
D= np.diag(d)

Degree matrix = \(I\)

array([[1., 0., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 1.]])

lst = []
for i in range(6):
    for j in range(6):
        if w[i,j] == 1:
            lst.append([i,j])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)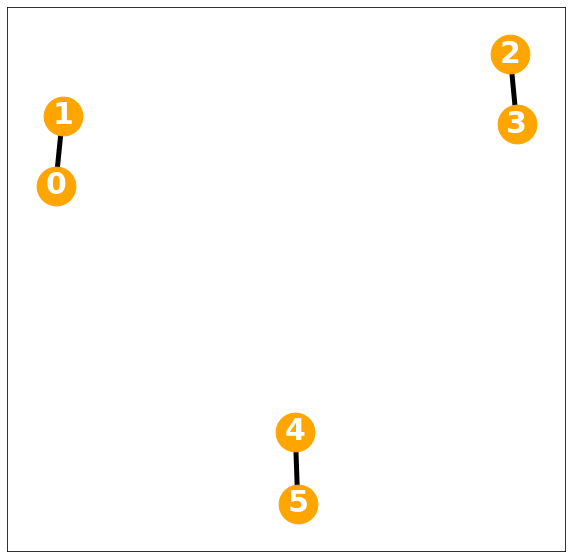

2-regular graph

w = np.array([
       [0., 1., 1., 0., 0., 0.],
       [1., 0., 1., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 1.],
       [0., 0., 0., 1., 0., 1.],
       [0., 0., 0., 1., 1., 0.]])

d= w.sum(axis=1)
D= np.diag(d)

Degree matrix = \(2I\)

array([[2., 0., 0., 0., 0., 0.],
       [0., 2., 0., 0., 0., 0.],
       [0., 0., 2., 0., 0., 0.],
       [0., 0., 0., 2., 0., 0.],
       [0., 0., 0., 0., 2., 0.],
       [0., 0., 0., 0., 0., 2.]])

lst = []
for i in range(6):
    for j in range(6):
        if w[i,j] == 1:
            lst.append([i,j])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)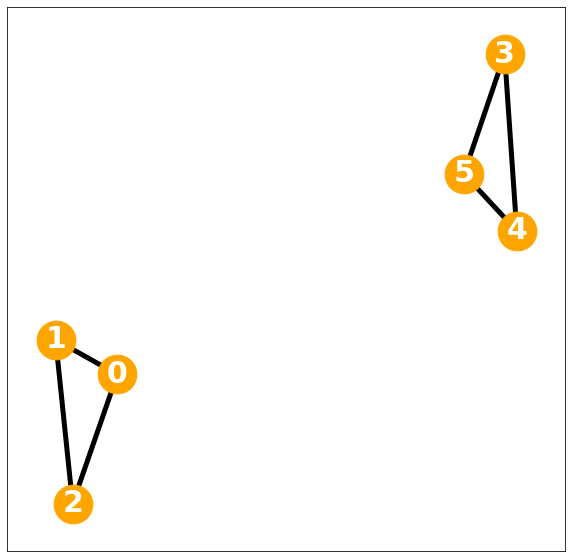

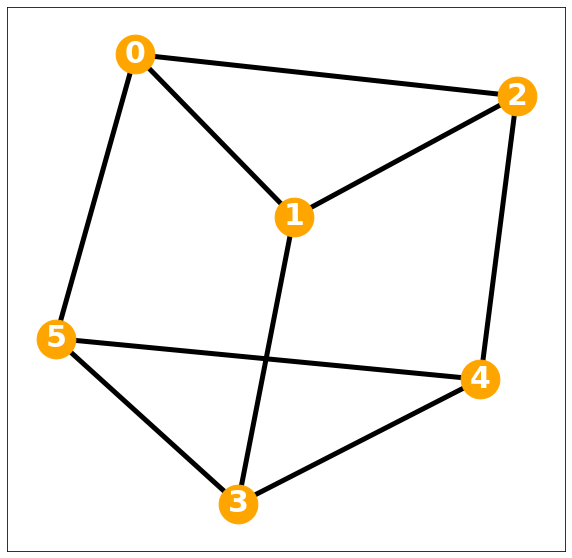
3-regular graph

w = np.array([
       [0., 1., 1., 0., 0., 1.],
       [1., 0., 1., 1., 0., 0.],
       [1., 1., 0., 0., 1., 0.],
       [0., 1., 0., 0., 1., 1.],
       [0., 0., 1., 1., 0., 1.],
       [1., 0., 0., 1., 1., 0.]])

d= w.sum(axis=1)
D= np.diag(d)

Degree matrix = \(3I\)

array([[3., 0., 0., 0., 0., 0.],
       [0., 3., 0., 0., 0., 0.],
       [0., 0., 3., 0., 0., 0.],
       [0., 0., 0., 3., 0., 0.],
       [0., 0., 0., 0., 3., 0.],
       [0., 0., 0., 0., 0., 3.]])

lst = []
for i in range(6):
    for j in range(6):
        if w[i,j] == 1:
            lst.append([i,j])

G = nx.Graph()

G.add_edges_from(np.array(lst))

plt.figure(figsize=(10, 10)) 
nx.draw_networkx(G, with_labels=True, font_weight='bold', node_color='orange', node_size=1500, font_color='white', font_size=30,width=5)