정리

import random

def estimate_pi(num_samples):
    inside_circle = 0

    for _ in range(num_samples):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)

        distance = x**2 + y**2

        if distance <= 1:
            inside_circle += 1

    pi_estimate = (inside_circle / num_samples) * 4
    return pi_estimate

# 시뮬레이션에 사용할 샘플 수 설정
num_samples = 1000000

# 파이 근사값 계산
pi_approximation = estimate_pi(num_samples)

# 결과 출력
print(f"Approximated Pi: {pi_approximation}")

Approximated Pi: 3.141964

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

# 랜덤 워크 생성
np.random.seed(42)
t = 300
y = np.cumsum(np.random.randn(t))

# 차분
diff_y = np.diff(y)

# ARIMA 모델 생성
model = ARIMA(diff_y, order=(1, 0, 0))  # ARIMA(p, d, q)에서 d가 차분의 차수를 의미합니다.
result = model.fit()

# 미래 예측
n = 1  # 다음 시점 하나만 예측
forecast = result.forecast(steps=n)

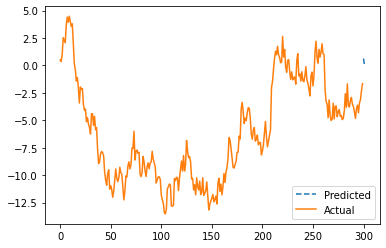
# 예측 결과 시각화
plt.plot(np.arange(t, t + n + 1), np.concatenate(([diff_y[-1]], forecast)), label='Predicted', linestyle='dashed')
plt.plot(np.arange(t), y, label='Actual')
plt.legend()
plt.show()