14wk: 이산형과 연속형의 통합

GUEBIN CHOI

2023-06-06

강의 영상

Import

import numpy as np
import matplotlib.pyplot as plt

일반화된 밀도함수

- 라돈니코딤 정리는 꼭 르벡메져일 경우에만 성립하는 것이 아니다.

이산확률변수

- 예제1 – 베르누이 (with 카운팅메져)

아래와 같은 함수를 고려하자.

\[F_X(x) = \begin{cases} 0 & x<0 \\ \frac{1}{2} & 0 \leq x <1 \\ 1 & x \geq 1 \end{cases}\]

def F_X(x):
    if x < 0:
        return 0
    elif 0 <= x < 1:
        return 1/2
    else:
        return 1

# 그래프를 그릴 x 범위 설정
x = np.linspace(-1, 2, 1000)

# 누적분포함수 계산
y = [F_X(val) for val in x]

# 그래프 그리기
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('F_X(x)')
plt.title('Cumulative Distribution Function')
plt.grid(True)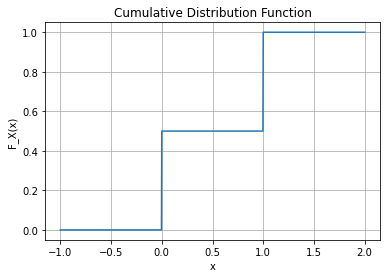

이제 $S=\{0,1\}$, ${\cal S}=\{\emptyset, \{0\},\{1\},\{1,2\}\}$로 구성된 measurable space $(S,{\cal S})$를 생각하자. 함수 $\tilde{\mu}_X: {\cal S} \to [0,1]$를 아래와 같이 정의하면

$\tilde{\mu}_X(\emptyset)= 0$
$\tilde{\mu}_X(\{0\})= \frac{1}{2}$
$\tilde{\mu}_X(\{1\})= \frac{1}{2}$
$\tilde{\mu}_X(\{0,1\})= 1$

$\tilde{\mu}_X(\emptyset)= 0$ $\rightarrow$ $P(\emptyset)$
$\tilde{\mu}_X(\{0\})= \frac{1}{2}$ $\rightarrow$ $P(H)$
$\tilde{\mu}_X(\{1\})= \frac{1}{2}$ $\rightarrow$ $P(T)$
$\tilde{\mu}_X(\{0,1\})= 1$ $\rightarrow$ $P(\Omega)$

$\to$ $mu_x : \cal{R} \to [0,1]$으로 착각할 수 있지만 여기서는 $\cal{S} \to [0,1]$로 정의하였으므로 다르다.

함수 $\tilde{\mu}_X$는 $(S,{\cal S})$에서의 메져가 되며, 이것은 $F_X$에 대응하는 분포 ${\mu}_X$와 같은 역할을 한다. 이제 measurable space $(S,{\cal S})$에 대하여 아래와 같은 함수 $\#: {\cal S} \to \mathbb{R}$을 고려하자.

$\#(\emptyset)=0$
$\#(\{0\})= 1$
$\#(\{1\})= 1$
$\#(\{0,1\})= 2$

단순히 말하면 $\#(A)$ = 집합 $A$의 원소 수라고 할 수 있다.

이때 함수 $\#$은 $(S,{\cal S})$ 에서의 메져가 되며, 이러한 메져를 특별히 카운팅메져(counting measure) 라고 한다. 이제 아래의 함수 $f_X:S \to \mathbb{R}$를 고려하자.

$f_X(0)=\frac{1}{2}$
$f_X(1)=\frac{1}{2}$

함수 $f_X$는 카운팅메져 $\#$에 대한 $\tilde{\mu}_X$의 라돈니코딤 도함수임을 보여라.

(해설)

$\tilde{\mu}_X$, $\#$는 모두 $(S,{\cal S})$ 에서의 $\sigma$-finite 메져이다.
$\tilde{\mu}_X << \#$이 성립한다. 따라서 적당한 ${\cal S} - {\cal R}^+$ measurable function이 존재하여 라돈니코딤 도함수의 조건을 만족함을 알 수 있다.
우리가 생각하는 후보는 $f_X$인데 이것이 만약에 (1) ${\cal S} - {\cal R}^+$ 가측함수이고 (2) 라돈니코딤 도함수의 조건¹을 만족한다면 $f_X$는 카운팅메져 $\#$에 대한 $\mu$의 거의 유일한 (w.r.t. $\#$) 밀도함수라고 주장할 수 있다.
$f_X$는 ${\cal S} \to {\cal R}^+$ 가측함수이다. (simple function)
$\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#=\sum_{x \in B} f_X(x)$ 를 만족한다.

1. $\tilde{\mu}_X$, $\#$는 모두 $(S,{\cal S})$ 에서의 $\sigma$-finite 메져이다.

$\tilde{\mu}_x(S) = 1$이고, $\#(S) = 2$이니까 $\tilde{\mu}_x, \#(S)$는 finite msr가 된다. 따라서 $\sigma$-finite msr 이다.

$\tilde{\mu}_X << \#$이 성립한다. 따라서 적당한 ${\cal S} - {\cal R}^+$ measurable function이 존재하여 라돈니코딤 도함수의 조건을 만족함을 알 수 있다.

$\forall B \in \cal{S} : \#(B) = 0 \leftrightarrow \tilde{\mu}_x (B) = 0$임을 보이면 된다.
$\cal{S} = \{ \emptyset, \{0\}, \{1\}, \{0,1\} \}$이 있을때 위의 조건을 만족하는 것은 $\emptyset$ 뿐이다.
따라서 $\tilde{\mu}_x (B) = 0$이 된다.

우리가 생각하는 후보는 $f_X$인데 이것이 만약에 (1) ${\cal S} - {\cal R}^+$ 가측함수이고 (2) 라돈니코딤 도함수의 조건²을 만족한다면 $f_X$는 카운팅메져 $\#$에 대한 $\mu$의 거의 유일한 (w.r.t. $\#$) 밀도함수라고 주장할 수 있다.

1,2로 확인 $\to$ 적당한 가측함수 $f$가 존재하여 $\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#$ $\dots \star$을 만족하는 $f$가 거의 유일하게 존재한다.

${\cal S} - {\cal R}^+$ 가측함수이고 - Check

simple function 이기 때문에 measurable function이다.
$f_X(0)=\frac{1}{2}$와 $f_X(1)=\frac{1}{2}$는 모두 $\frac{1}{2}$로 하나로만 나타나니까 simple function으로 표현 가능

라돈니코딤 도함수의 조건³ Check

$B = \emptyset$ : LHS = 0, RHS = $\int_{\emptyset} f_X d\#$ = 0
$B = \{0,1\}$ : LHS = $\mu(B) = 1$, RHS = $\int_{\{0,1\}} f_X d\# = \int_{\{0\}} f_X d\# + \int_{\{1\}} f_X d\# = \frac{1}{2} + \frac{1}{2} = 1$
- $f(0) \# \{0\} = \frac{1}{2} \times 1 = \frac{1}{2}$
- $f(1) \# \{1\} = \frac{1}{2} \times 1 = \frac{1}{2}$

$f_X$는 ${\cal S} \to {\cal R}^+$ 가측함수이다. (simple function)

3에서 확인 가능

$\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#=\sum_{x \in B} f_X(x)$ 를 만족한다.

3에서 확인 가능

- 예제1에서 제안한 $f_X$의 경우 어떠한 의미에서는 밀도함수라고 해석할 수 있다.

학부수준의 이해: 이산형확률변수는 확률질량함수를 가지며, 연속형확률변수는 확률밀도함수를 가진다.
대학원수준의 이해: 이산형확률변수의 밀도함수는 $\#$에 대한 라돈니코딤 도함수로 해석할 수 있으며, 연속형확률변수의 밀도함수는 $\lambda$에 대한 라돈니코딤 도함수로 해석할 수 있다.

- 찝찝한점1: 예제1에서는 왜 $\mu_X$ 대신에 $\tilde{\mu}_X$를 사용했을까?

사실 예제1에서의 $\tilde{\mu}_X$는 $F_X$에 대응하는 distribution $\mu_X$와 유사하지만 미세한 차이가 있음

$\mu_X:{\cal R} \to [0,1]$

$\mu_X(\emptyset)=0$
$\mu_X(\{0\})=\frac{1}{2}$
$\mu_X(\{1\})=\frac{1}{2}$
$\mu_X(\{0,1\})=1$
$\mu_X(B)=0$ , $B \in {\cal R} - \{0,1\} - \{0\} - \{1\}$

$\tilde{\mu}_X:{\cal S} \to [0,1]$

$\tilde{\mu}_X(\emptyset)= 0$
$\tilde{\mu}_X(\{0\})= \frac{1}{2}$
$\tilde{\mu}_X(\{1\})= \frac{1}{2}$
$\tilde{\mu}_X(\{0,1\})= 1$

- 찝찝한점2: 예제1에서는 왜 $(\mathbb{R},{\cal R})$를 고려하지 않고 $(S,{\cal S})$를 고려하였을까?

- 찝찝한점의 해결:

라돈니코딤 도함수의 존재에 필요한 조건 중 하나는 라돈니코딤 도함수를 정의하는 두개의 메져⁴ $\sigma$-finite measure이어야 한다는 것임.
$\mu_X,\lambda$ on $(\mathbb{R},{\cal R})$을 고려 $\Rightarrow$ $\mu_X,\lambda$ 은 모두 $(\mathbb{R},{\cal R})$에서 $\sigma$-finite 조건을 만족함.
$\tilde{\mu}_X,\#$ on $(S,{\cal S})$을 고려 $\Rightarrow$ $\tilde{\mu}_X,\#$ 은 모두 $(S,{\cal S})$에서 $\sigma$-finite 조건을 만족함.
$\mu_X, \#$ on $(\mathbb{R},{\cal R})$을 고려 $\Rightarrow$ $\mu_X$ 는 $(\mathbb{R},{\cal R})$에서 $\sigma$-finite 하지만 $\#$는 $(\mathbb{R},{\cal R})$에서 $\sigma$-finite 하지 않음.

따라서, $(\mathbb{R},{\cal R})$에서의 두 메져 $\mu_X,\lambda$를 고려하거나, $(S,{\cal S})$에서의 두 메져 $\tilde{\mu}_X,\#$ 를 고려해야 라돈니코딤 도함수를 따져볼 수 있다.

모티브: 그런데 $(S,{\cal S})$ 말고 그냥 $(\mathbb{R},{\cal R})$에서 적당히 $\mu_X, \tilde{\#}$를 고려할 수는 없을까?

의문: $\tilde{\mu}_X$대신 $\mu_X$를 고려한다면?

$\mu_X,\lambda$ on $(\mathbb{R},{\cal R})$ 에서 $\mu_X,\lambda$가 $\sigma$-finite 하다면,

$\rightarrow$ $\frac{d\mu_x}{d\lambda} = pdf$(연속형 확률변수의)의 일반화된 버전

$\tilde{\mu}_X,\#$ on $(S,{\cal S})$ 에서 $\tilde{\mu}_X,\#$가 $\sigma$-finite 하다면,

$\rightarrow$ $\frac{d \tilde{\mu}_x}{d\#} = pmf$ 로 쓸 수 있지만, 이렇게 쓰지 말고 아래처럼 쓰고 싶다.

$\mu_X, \#$⁵ on $(\mathbb{R},{\cal R})$ 에서 $\mu_X, \#$가 $\sigma$-finite 하다면,

$\rightarrow$ $\frac{d\mu_x}{d \#} = pmf$

$\rightarrow$ 하지만, $\#(\mathbb{R}) = \infty$이므로 finite 하지 않고 $\sigma$-finite 하지 않다.

$\star$ $\sigma$-finite의 조건

$\lambda$가 $(\mathbb{R},\cal{R})$에서 $\sigma$-finite하는지 확인
$\lambda$ is $\sigma$-finite msr on $(\mathbb{R},\cal{R})$인지 보이기.
$\leftrightarrow$ $A_1,A_2, \dots$, st (1) $\cup^\infty_{n=1} A_n = \cal{R}$ & (2) $ (A_n) < , n $를 만족해야 한다.
$A_n = (-n,n)$의 열린 구간으로 보면,

$\cup^\infty_{n=1} A_n = \cal{R}$은 $\cup^\infty_{n=1} A_n = \mathbb{R}$로 만족함을 보임.
$ (A_n) < , n $은 $\lambda(A_n) = 2n < \infty \forall n \in \mathbb{N}$ 로 만족함을 보임.

$\rightarrow$ 카운팅 메져 $\#$으로 바꾼다면? $\#(A_n) = \infty$하여 $(\mathbb{R},\cal{R})$에서 $\sigma$-finite하지 않다.

정리

$\lambda$는 $(\mathbb{R},\cal{R})$에서 $\sigma$-finite msr

$\#$는 $(\mathbb{R},\cal{R})$에서 $\sigma$-finite msr가 아님

$\#$는 $(\mathbb{N},2^{\mathbb{R}})$에서 $\sigma$-finite msr

모티브: 그런데 $(S,{\cal S})$ 말고 그냥 $(\mathbb{R},{\cal R})$에서 적당히 $\mu_X, \tilde{\#}$를 고려할 수는 없을까?

- 예제2 – 베르누이 (with 디렉메져)

아래와 같은 함수를 고려하자.

\[F_X(x) = \begin{cases} 0 & x<0 \\ \frac{1}{2} & 0 \leq x <1 \\ 1 & x \geq 1 \end{cases}\]

def cumulative_distribution(x):
    if x < 0:
        return 0
    elif 0 <= x < 1:
        return 1/2
    else:
        return 1

x = np.linspace(-1, 2, 1000)
y = np.vectorize(cumulative_distribution)(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('F_X(x)')
plt.title('Cumulative Distribution Function')
plt.grid(True)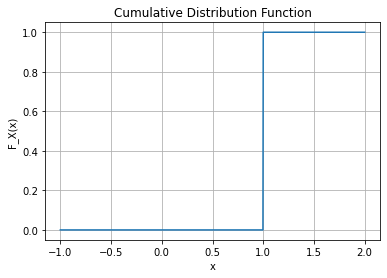

$F_X$에 대응하는 분포 $\mu_X:{\cal R} \to [0,1]$를 고려하자.

$\mu_X(\emptyset)=0$
$\mu_X(\{0\})=\frac{1}{2}$
$\mu_X(\{1\})=\frac{1}{2}$
$\mu_X(\{0,1\})=1$
$\mu_X(B)=0$ , $B \in {\cal R} - \{0,1\} - \{0\} - \{1\}$

그리고 아래와 같은 메져를 고려하라. $\#_X: {\cal R} \to \mathbb{N}$ 을 고려하자.

$\#_X(\emptyset)=0$
$\#_X(\{0\})=1$
$\#_X(\{1\})=1$
$\#_X(\{0,1\})=2$
$\#_X(B)=0$, $B \in {\cal R}-\{0,1\}-\{0\}-\{1\}$

$X$가 각각 값이 나올 확률

$X = 0$ $wp = \frac{1}{2}$
$X = 1$ $wp = \frac{1}{2}$

$X$의 support 인 경우는 1, 아닌 경우는 모두 0

$\#_X(\emptyset)=0$
$\#_X(\{0\})=1$
$\#_X(\{1\})=1$
$\#_X(\{0,1\})=2$
$\#_X(B)=0$, $B \in {\cal R}-\{0,1\}-\{0\}-\{1\}$
- 즉, 4가지 경우는 $\#$와 같고, 그 외의 case는 0으로 정의된다.
- ex) $\#(\{0,1,2\}) = 3$이지만 $\#_X(\{0,1,2\}) = \#_X(\{0,1)\} + \#_X(\{,2\}) = 2+ 0 = 2$가 된다.
- $\#_X(\mathbb{R})$은 $\sigma$-finite 하다.
  - $\#_X(\{0,1\}) + \#_X(\mathbb{R} - \{0,1\}) = 2+0 = 2$이므로 finite 하기 때문에 $\sigma$-finite 하다.
- 절대연속이기도 하다.
  - $\forall B \in \cal{R}$에 대해 $\#_X(B) = \mu_X(B)= 0$임을 보이면 되는데, 둘 다 0이라는 값이 나오기 때문에 절대연속 조건 만족한다.

이때 함수 $\#_X:{\cal R} \to \mathbb{N}$ 는 $(\mathbb{R},{\cal R})$ 에서의 $\sigma$-finite 메져가 된다. 또한 $\mu_X << \#_X$ 가 성립한다.⁶ 이제 아래의 함수 $f_X:\mathbb{R} \to \mathbb{R}^+$를 고려하자.

\[f_X(x)=\begin{cases} \frac{1}{2} & x=0,1 \\ 0 & o.w. \end{cases}\]

함수 $f_X$는 ${\cal R}-{\cal R}^+$ 가측함수이고 (simple function 이므로)

\[\forall B \in {\cal R}: \mu_X(B)= \int_B fd\#_X\]

를 만족한다. 따라서

\[f_X=\frac{d\mu_X}{d\#_X}\]

이다. 즉 $f_X$는 $\#_X$에 대한 $\mu_X$의 라돈니코딤 도함수로 해석할 수 있다.

$f_X(x)=\begin{cases} \frac{1}{2} & x=0,1 \\ 0 & o.w. \end{cases}$ 두 경우만 있으므로 simple function 이고 따라서 measurable function이다.

$\forall B \in {\cal R}: \mu_X(B)= \int_B fd\#_X$이 성립하는 예제

ex) $\mu_X(\{0\}) = \int_{\{0\}} f d \#_X = f(0) \#_X(\{0\}) = \frac{1}{2} \times 1 = \frac{1}{2}$
$B = (-\infty, 0 ] \cup [1,\infty)$에 대하여 $\mu_X(B) = \int_B f d \#_X$를 만족하는지 따지자.⁷

$B = (-\infty,0) \cup \{0\} \cup \{1\} \cup (1,\infty) = B_1 \uplus\{0\} \uplus \{1\} \uplus B_2$

LHS = $\mu_X(\{0\} ).+ \mu_X(\{1\})$

RHS = $f(0) \#(\{0\} + f(1)\#(\{1\})$

- 정의 (디렉메져): 가측공간 $(\mathbb{R}, {\cal R})$에서 디렉메져 $\delta_x$는

\[\forall B \in {\cal R}: ~\delta_{x}(B)=\mathbb{1}_B(x)=\mathbb{1}(x \in B)\]

로 정의되는 메져이다.

- 디랙메져의 표현법에 따르면 예제2의 경우 $\#_X := \delta_0 + \delta_1$ 로 표현할 수 있다. 여기에서 $\delta_x$는 $(\mathbb{R},{\cal R})$에서의 디랙메져이다.

- 꼭 베르누이와 같은 상황이 아니라도 임의의 이산확률변수 $X$에 대한 분포 $\mu_X$를 dominating하는 적절한 $\sigma$-finite한 메져 $\#_X$를 $(\mathbb{R}, {\cal R})$에서 정의할 수 있다. 예를들면 주사위예제의 경우

\[\#_X = \delta_1+\delta_2+\delta_3+\delta_4+\delta_5+\delta_6\]

와 같은 방식으로 정의할 수 있다. 즉 임의의 이산확률변수 $X$에 대하여 아래를 만족하는 $\#_X$를 항상 잡을 수 있다.

$\#_X$ is $\sigma$-finite
$\mu_X << \#_X$

따라서 $\frac{d\mu_X}{d\#_X}$는 언제나 잘 정의되며 이는 우리가 알고 있는 pmf의 정의와 일치한다.

디렉메져, $\cal{S}_x(B) \to 0,1$

$x\in B$ $\rightarrow 1$
$x\notin B$ $\rightarrow 0$
- $\delta_0(\{0\}) = 1$, 0이 포함되니까 1
- $\delta_0(\{1\}) = 0$, 0이 포함되지 않으니까 0
- $\delta_0([0,1]) = 1$, 0이 포함되니까 1
- $\delta_0((0,1)) = 0$, 0이 포함되지 않으니까 0

따라서 위의 $\#_X$를 디렉메져로 정의한다면, $\#_X: \delta_0 + \delta_1$

$(\delta_0 + \delta_1)(\{0,1\}) = \delta_0 (\{0,1\}) + \delta_1(\{0,1\}) = 1+1=2$

- 결국 이산형 확률변수의 밀도함수를 설명하는 방법은 크게 3가지가 있는 셈이다.

이산형확률변수는 밀도함수가 없다.
이산형확률변수의 밀도함수는 $\frac{d}{d\#}\tilde{\mu}_X$ 으로 정의할 수 있다.
이산형확률변수의 밀도함수는 $\frac{d}{d\#_X}\mu_X$ 으로 정의할 수 있다.

설명1,2,3은 각각의 장단점이 있다.

설명1: 라돈니코딤 도함수에 대한 이해가 없어도 된다는 점에서 장점이 있다. (그래서 학부수준에서는 가장 일반적으로 사용하는 설명)

설명2: 연속형은 르벡메져에 대한 라돈니코딤 도함수, 이산형은 카운팅메져에 대한 라돈니코딤 도함수로 구분하여 설명할 수 있다는 점에서는 클리어하지만 분포함수 $\mu_X$를 활용하지 못한다는 점과 그에 따라서 이산형 확률변수의 support $S$에 맞추어 가측공간 $(S,{\cal S})$를 재설정해야한다는 불편함이 있다. 이러한 방식으로 유도되는 베르누이 분포의 pmf는 아래와 같이 정의된다.

$f_X(x)=p_X(x)=\begin{cases} 1-p & x=0 \\ p & x=1 \end{cases}$

설명3: 연속형은 르벡메져에 대한 라돈니코딤 도함수, 이산형은 카운팅메져에 대한 라돈니코딤 도함수로 구분하여 설명할 수는 없으며 확률변수 $X$에 따라서 $\#_X$를 그때 그때 정의해야하는 지저분함이 있다. 하지만 분포함수 $\mu_X$를 활용할 수 있고 가측공간 $(\mathbb{R},{\cal R})$를 그대로 활용한다는 장점이 있다. 이러한 방식으로 유도되는 베르누이분포의 pmf는 아래와 같이 정의된다.

$f_X(x)=p_X(x)=\begin{cases} 1-p & x=0 \\ p & x=1 \\ 0 & o.w. \end{cases}$

이산형확률변수는 밀도함수가 없다.

$\mu_X << \lambda$ $\mu_X$가 르벡메져에 대해 $X$에 대해 연속이 아니기 때문에 밀도함수가 없다.

이산형확률변수의 밀도함수는 $\frac{d}{d\#}\tilde{\mu}_X$ 으로 정의할 수 있다.

꼭 르벡메져로 볼 필요 없음
카운팅 msr로 보고 $\tilde{\mu}_X$로 보겠다.
카운팅 msr를 수정하지 않고 그대로 쓸 수 있다는 장점
$\mu_X$ 대신 $\tilde{\mu}$ 써야 한다는 단점
$\frac{d \tilde{\mu}_X}{d \#_X}$가 모두 $(\mathbb{S},\cal{S}$에서 정의되기 때문에 support를 실수 전체로 잡을 필요가 없다.

이산형확률변수의 밀도함수는 $\frac{d}{d\#_X}\mu_X$ 으로 정의할 수 있다.

카운팅 msr로 보고 $\mu_X$로 보겠다.
$\mu_X$ 그대로 쓴다는 장점
카운팅 msr를 수정해야 한다는 단점
$\frac{d \mu_X}{d \#_X}$가 모두 $(\mathbb{R},\cal{R}$에서 정의되기 때문에 support를 실수 전체로 잡아야 한다.

혼합형확률변수

- 예제1: 아래와 같은 분포함수 $F_X$를 고려하자.

\[F_X(x) = \begin{cases} 0 & x< 0 \\ \frac{1}{2} & 0 \leq x < \frac{1}{2} \\ x & \frac{1}{2} \leq x \leq 1 \\ 1 & x>1 \end{cases}\]

def cumulative_distribution(x):
    result = []
    for val in x:
        if val < 0:
            result.append(0)
        elif 0 <= val < 1/2:
            result.append(1/2)
        elif 1/2 <= val <= 1:
            result.append(val)
        else:
            result.append(1)
    return result

x = np.linspace(-1, 2, 1000)
y = cumulative_distribution(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('F_X(x)')
plt.title('Cumulative Distribution Function')
plt.grid(True)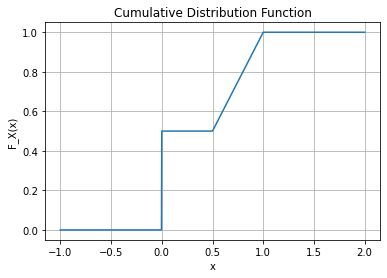

이 분포함수는 동전을 던져 앞면이 나오면 $X=0$으로 결정하고 뒷면이 나오면 균등분포 $[0.5,1]$에서 확률변수 $X$를 생성하는 실험을 상상하면 쉽게 이해할 수 있다. 아래와 같은 함수

\[f_X(x) = \begin{cases} \frac{1}{2} & x=0 \\ 1 & \frac{1}{2} \leq x \leq 1 \\ 0 & o.w. \end{cases}\]

가 $F_X$의 밀도함수가 될 수 있음을 설명하라.

(해설)

$\nu:= \lambda + \delta_0$ 이라고 정의하자.
$\nu$는 $\sigma$-finite 하며 $\mu_X << \nu$ 를 만족한다.
함수 $f_X(x)$는 가측함수이며 (simple function) $\forall B \in {\cal R}$에 대하여 아래를 만족한다.

\[\mu_X(B)=\int_B f_X d\nu =\int_B f_X d(\lambda+\delta_0)=\int_B f_X d\lambda + \int_B f_X d\delta_0\]

$\nu:= \lambda + \delta_0$ 이라고 정의하자.

$\nu:= \lambda + \delta_0$의 의미 $\rightarrow$ $\forall B \in \cal{R}$: $\nu(B) = \lambda(B) + \delta_0(B)$이렇게 더할 것이다는 뜻

$\nu$는 $\sigma$-finite 하며 $\mu_X << \nu$ 를 만족한다.

$\lambda$가 finite하고, $\delta_0$가 $\sigma$-finite 하여 $\nu$도 $\sigma$-finite 할 것이다.
$\nu$ is $\sigma$-finite on $(\mathbb{R},\cal{R})$

pf. $A_n = (-n,n)$ open range로 잡으면, $\nu(A_n) = \lambda(A_n) + \delta(A_n) = 2n+1$⁸

$\because \forall n \in \mathbb{N}$ $\nu(A_n) = 2n + 1 < \infty$

그리고 $\cup^\infty_{n=1} A_n = \mathbb{R}$ 따라서 $\sigma$-finite 하다.

$\nu(B) = 0 \leftrightarrow \mu_X(B) = 0$으로 절대연속임을 보이자.

$(\lambda + \delta_0) (B) = 0$⁹

$\lambda(B) + \delta_0(B) = 0$¹⁰

따라서 $\lambda(B) = 0$ & $\delta_0(B) = 0$

$\mu_X(B) = \mu_X(B - \{0\})$¹¹ $+ \mu_X(\{0\})$¹² $= 0 + 0 = 0$

함수 $f_X(x)$는 가측함수이며 (simple function) $\forall B \in {\cal R}$에 대하여 아래를 만족한다.

simple function 이기 때문에 가측함수
모든 구간에서 증명이 어려워 특정 집합 $B = (-\infty,x]$에서 증명 후 $\pi-\lambda$-system 사용하여 증명

$B = (-\infty,x]$,

$\mu_X(B) = F_X(x)$가 됨.

$x<0, \mu_X(B) = F_X(x) = 0$

$\mu_X(B) = 0$

$\int_B f_X d\lambda + \int_B f_X d\delta_0=0$

$\rightarrow$ 성립

$x=0, F_X(X) = \frac{1}{2}$

$\mu_X(B) =F_X(X)= \frac{1}{2}$

$\int_{-\infty}^0 f_X d\lambda + \int_{-\infty}^0 f_X d\delta_0 = 0 + \int_{\{0\}} f_X d \delta_0 = f_X(0) \delta_0(\{0\}) = \frac{1}{2} \times 1 = \frac{1}{2}$

$\rightarrow$ 성립

$0<x<\frac{1}{2}$ , $F_X(X)= \frac{1}{2}$

$\mu_X(B) = F_X(X) = \frac{1}{2}$

$\int_{-\infty}^x f_X d\lambda$¹³ $+ \int_{-\infty}^x f_X d\delta_0 = 0 + \int_{\{0\}}^x f_X d\delta_0 = f_X(0) \delta_X(\{0\}) = \frac{1}{2} \times 1 = \frac{1}{2}$

$\rightarrow$ 성립

$\frac{1}{2} \le x \le 1$ $F_X(x) = x$

$\mu_X(B) = F_X(x) = x$

$\int_{-\infty}^x f_X d\lambda + \int_{-\infty} f_X d\delta_0 = \int_{-\infty}^x f_X d\lambda + \frac{1}{2} = \int_{\frac{1}{2}}^1 1 dx + \frac{1}{2} = x - \frac{1}{2} + \frac{1}{2}$¹⁴

$\rightarrow$ 성립

$x>1$ $F_X(x) = \mu_X(x) = 1$

$\mu_X(B) = F_X(x) = 1$

$\int_{-\infty}^x f_X d\lambda + \int_{-\infty}^x f_X d\delta_0 = \int_{\frac{1}{2}}^1 1 dx + \frac{1}{2} = \frac{1}{2}+ \frac{1}{2}$

위의 3에 대한 추가설명.

결국 임의의 $B=(-\infty,x]$와 같은 꼴에서 $\mu_X(B) = \int_Bf_Xd\lambda + \int_B f_Xd\delta_0$ 임을 보이면 된다.

편의상 아래와 같이 정의하자.

$LHS = \mu_X(B)$
$RHS_1 = \int_B f_Xd\lambda$
$RHS_2 = \int_B f_Xd\delta_0$

case1: $x < 0$

$LHS = F_X(x)=0$
$RHS_1 = 0$
$RHS_2 = 0$

case2: $x = 0$

$LHS = F_X(x)=\frac{1}{2}$
$RHS_1 = \int_{-\infty}^0f_X(x)dx = 0$
$RHS_2 = \int_{\{0\}}f_Xd\delta_0 = f_X(0)\delta_0(\{0\}) = \frac{1}{2}$

case3: $0<x< \frac{1}{2}$

$LHS = F_X(x)=\frac{1}{2}$
$RHS_1 = \int_{-\infty}^{0}f_X(x)dx+ \int_{0}^{x}f_X(x)dx= 0$
$RHS_2 = \int_{\{0\}}f_Xd\delta_0 = f_X(0)\delta_0(\{0\}) = \frac{1}{2}$

case4: $\frac{1}{2}<x< 1$

$LHS = F_X(x)=x$
$RHS_1 =\int_{-\infty}^{1/2}f_X(x)dx+ \int_{1/2}^xf_X(x)dx = \int_{1/2}^xf_X(x)dx=\int_{1/2}^xdx= x-\frac{1}{2}$
$RHS_2 = \int_{\{0\}}f_Xd\delta_0 = f_X(0)\delta_0(\{0\}) = \frac{1}{2}$

case5: $x>1$

$LHS = F_X(x)=1$
$RHS_1 =\int_{-\infty}^{1/2}f_X(x)dx+ \int_{1/2}^{1}f_X(x)dx = \int_{1/2}^1f_X(x)dx=\int_{1/2}^1dx= 1-\frac{1}{2}$
$RHS_2 = \int_{\{0\}}f_Xd\delta_0 = f_X(0)\delta_0(\{0\}) = \frac{1}{2}$

르벡분해정리

- Thm: 분포함수의 정의¹⁵를 만족하는 임의의 $F$는 항상 아래와 같이 분해가능하다.

\[F = F_{ac}+F_{pp}+F_{sing}\]

여기에서 $F_{ac}$는 르벡메져에 대하여 절대연속이고 $F_{pp}$는 카운팅메져에 대하여 절대연속이다. 따라서 $F_{ac}$와 $F_{pp}$는 각각 르벡메져와 카운팅메져에 대응하는 밀도함수가 존재한다. $F_{sing}$는 칸토어분포와 같이 밀도함수가 존재하지 않는 경우이다.

- 의미: $F_{ac}$는 우리가 일반적으로 생각하는 singular하지 않은 연속함수를 상상하면 된다.¹⁶ $F_{pp}$는 완벽한 불연속이며 오직 jump를 통해서만 증가하는 함수라 생각하면 된다. 즉 우리가 익숙한 이산형확률변수의 cdf를 상상하면 된다.

- 이론: $F_{pp}$는 기껏해야 countable한 불연속점을 가진다. (jump 하는 point는 countable이라는 의미, 결국 이산형확률변수의 support는 countable이라는 의미)

- 이론: 분포함수 정의를 만족하는 임의의 $F$가 아래와 같다면

\[F=F_{ac}\]

$F$에 대응하는 연속형 확률변수 $X$가 존재하고 그에 대응하는 pdf가 존재한다.

- 이론: 분포함수 정의를 만족하는 임의의 $F$가 아래와 같다면

\[F=F_{pp}\]

$F$에 대응하는 이산형 확률변수 $X$가 존재하고 그에 대응하는 (일반화된) pdf 혹은 pmf가 존재한다.

- 이론: 분포함수 정의를 만족하는 임의의 $F$가 아래와 같다면

\[F=F_{ac}+F_{pp}\]

$F$에 대응하는 혼합형 확률변수 $X$가 존재하고 그에 대응하는 (일반화된) pdf가 존재한다.

기대값

- 예제1: $(\Omega,{\cal F},P)$를 확률공간이라고 하고 $\Omega=\{H,T\}$, ${\cal F}=2^\Omega$, $P(H)=P(T)=\frac{1}{2}$라고 하자.¹⁷ 확률변수 $X(H)=0$, $X(T)=1$를 정의하자. 이 확률변수의 기대값 $\mathbb{E}(X)$를 계산하여 보자.

$X$	$X=0$	$X=1$
$P(X=x)$	$\frac{1}{2}$	$\frac{1}{2}$

(풀이)

아래와 같이 계산할 수 있다. (고등학교 수준)

\[\mathbb{E}(X)= 0 \times \frac{1}{2} + 1\times \frac{1}{2}\]

이를 다른표현으로 써보면

$\mathbb{E}(X)= 0 \times (P\circ X^{-1})(\{0\}) + 1\times (P\circ X^{-1})(\{1\})$
$\mathbb{E}(X)= 0 \times \mu_X(\{0\}) + 1\times \mu_X(\{1\})$
$\mathbb{E}(X)= \sum_{x=0}^{1} x \times \mu_X(\{x\})$
$\mathbb{E}(X)= \int_{\mathbb{R}} x d\mu_X:=\int_{\mathbb{R}}xdF_X$
$\mathbb{E}(X)= \int_{\mathbb{R}} x \frac{d\mu_X}{d \#_X}d\#_X$
$\mathbb{E}(X)= \int_{\mathbb{R}} x p_X(x) d\#_X$
$\mathbb{E}(X)= \int_{\{0,1\}} x p_X(x) d\#_X$
$\mathbb{E}(X)= \sum_{x=0}^{1} xp_X(x)$

또는 아래와 같이 볼 수 도 있다.

$\mathbb{E}(X)= 0 \times (P\circ X^{-1})(\{0\}) + 1\times (P\circ X^{-1})(\{1\})$
$\mathbb{E}(X)= X(H) \times P(\{H\}) + X(T)\times P(\{T\})$
$\mathbb{E}(X)= \int X dP = \int_{\Omega} X dP = \int_{\omega \in \Omega}X(\omega)dP(\omega)$

위의 2 $\to$ 3에 대한 추가설명.

아래와 같은 함수 $f(x)$를 다시 고려하자.

\[f(x) = \begin{cases} 1 & \mathbb{Q} \cap [0,1] := A_1 \\ 0 & \mathbb{Q}^c \cap [0,1]: =A_2 \end{cases}\]

이 함수의 밑면적을 계산하기 위해서

$\int f d\lambda = 1 \times \lambda(A_1) + 0 \times \lambda(A_2)$

와 같은 계산을 정의하였다. 이를 다시 평이한 언어로 표현하면

적분값 = $\big($ $x \in A_1$에서의 함수값 $f(x)$ $\big)$ $\times$ $\big($ $A_1$을 $\lambda$로 잰 길이$\big)$ + $\big($ $x \in A_2$에서의 함수값 $f(x)$$\big)$ $\times$ $\big($ $A_2$을 $\lambda$로 잰 길이$\big)$

와 같은 방식으로 서술할 수 있다. 이제 가측함수 $f$에 대응하는 가측함수 $X$와, 메져 $\lambda$에 대응하는 메져 $P$를 고려하자. 즉

$f: [0,1] \to \mathbb{R}$ 인 measurable function such that $f(x) = \begin{cases} 1 & \mathbb{Q} \cap [0,1] := A_1 \\ 0 & \mathbb{Q}^c \cap [0,1]: =A_2 \end{cases}$
$X: \Omega \to \mathbb{R}$ 인 measurable function such that $X(\omega) = \begin{cases} 1 & \omega \in \{H\} := A_1 \\ 0 & \omega \in \{T\}: =A_2 \end{cases}$
$\lambda: {\cal R} \cap [0,1] \to [0,\infty]$ 는 measure on $([0,1], {\cal R} \cap [0,1])$.
$P : {\cal F} \to [0,1]$ 는 measure on $(\Omega, {\cal F})$.

에서 1대신 2를, 3대신 4를 생각하자는 의미이다. 그렇다면

적분값 = $\big($ $x \in A_1$에서의 함수값 $f(x)$ $\big)$ $\times$ $\big($ $A_1$을 $\lambda$로 잰 길이$\big)$ + $\big($ $x \in A_2$에서의 함수값 $f(x)$$\big)$ $\times$ $\big($ $A_2$을 $\lambda$로 잰 길이$\big)$

은 아래와 같이 대응하여 바꿀 수 있고

적분값 = $\big($ $\omega \in A_1$에서의 함수값 $X(\omega)$ $\big)$ $\times$ $\big($ $A_1$을 $P$로 잰 길이$\big)$ + $\big($ $\omega \in A_2$에서의 함수값 $X(\omega)$$\big)$ $\times$ $\big($ $A_2$을 $P$로 잰 길이$\big)$

이것은 다시

적분값 = $X(H)\times P(\{H\}) + X(T)\times P(\{T\})$

로 쓸 수 있다. 아래의 수식

$\int f d\lambda = 1 \times \lambda(A_1) + 0 \times \lambda(A_2)$

에 대응하여 다시 상기하면

$\int X dP = X(H)\times P(\{H\}) + X(T)\times P(\{T\})$

로 쓸 수 있다.

- 예제2: $(\Omega,{\cal F},P)$를 확률공간이라고 하고 $\Omega=[0,2\pi)$, ${\cal F}={\cal R} \cap [0,2\pi)$¹⁸, $P([0,x))=\frac{x}{2\pi}$라고 하자.¹⁹ 확률변수 $X(\omega)=\omega$에 대한 기대값 $\mathbb{E}(X)$를 계산하여 보자.

(풀이)

아래와 같이 계산할 수 있다. (고등학교 수준)

\[\mathbb{E}(X)=\int_0^{2\pi} x \frac{1}{2\pi}dx\]

이는 아래와 같이 변형할 수 있다.

$\mathbb{E}(X)= \int_0^{2\pi}xf_X(x)dx$, where $f_X(x)=\frac{1}{2\pi}$.
$\mathbb{E}(X)= \int_{\mathbb{R}}xf_Xd\lambda$.
$\mathbb{E}(X)= \int_{\mathbb{R}}x\frac{d\mu_X}{d\lambda}d\lambda$.
$\mathbb{E}(X)= \int_{\mathbb{R}}xd\mu_X:=\int_{\mathbb{R}}xdF_X$.

혹은 아래와 같이 변형할 수 있다.

$\mathbb{E}(X)= \int_{\mathbb{R}} xd\mu_X=\int_{[0,2\pi)}xd\mu_X(x)$
$\mathbb{E}(X)= \int_\Omega X(\omega)dP(\omega)=\int X dP$

위의 1 $\to$ 2, 즉 $\int_{[0,2\pi)} x d\mu_X(x) = \int_\Omega X dP$ 에 대한 이해의 추가설명 (강의에 너무 대충 설명해서..)

이 예제에서는 $X: [0,2\pi) \to [0,2\pi)$가 항등함수이므로,

\[\mu_X:= P \circ X^{-1} = P\]

가 성립하는 특이한 경우이다. 이는 이해를 용이하게 위해서 이 예제에서 특별하게 설정된 상황이다. 하지만 이 성질은 꼭 $X$가 항등함수가 아닐지라도 일반적으로 성립한다.

- 정의: $X$가 확률공간 $(\Omega,{\cal F},P)$에서 정의된 확률변수라고 할때 그 기대값 $\mathbb{E}(X)$는 아래와 같이 정의한다.

\[\mathbb{E}(X) = \int_{\Omega} X dP\]

여기에서 $X$는 이산형, 연속형, 혼합형등 어떠한 형태의 확률변수라도 상관없다. 위의 기대값은 항상 아래와 같이 표현할 수 있다.

\[\mathbb{E}(X) = \int_{\mathbb{R}} x d\mu_X:=\int_{\mathbb{R}} x dF_X\]

만약 $F_X$가 절대연속인 경우 (즉 $\mu_X << \lambda$ 인 경우) 아래와 같이 표현가능하다.

\[\mathbb{E}(X) = \int_{-\infty}^{\infty} xf_X(x)dx\]

만약에 $F_X$가 countable한 jump로만 구성되어 있다면 $\mu_X$는 jump point에서 support로 가지는 수정된 카운팅메져 $\#_X$에 대하여 절대연속이 되며 (즉 $\mu_X << \#_X$) 이 경우 기대값은 아래와 같이 표현가능하다.

\[\mathbb{E}(X) = \sum_{x}x p_X(x)\]

여기에서 $f_X(x)$와 $p_X(x)$는 각각 확률변수 $X$의 pdf, pmf가 된다. (혹은 $\lambda$와 $\#_X$에 대한 라돈니코딤 도함수)

- 요약

학부수준: 연속형확률변수의 기대값과 이산형확률변수의 기대값이 서로 다르게 정의된다.
대학원수준: 두 경우 모두 $\mathbb{E}(X) = \int X dP$로 정의된다.

Appendix

- 생존분석 강의노트

- WGAN

- 시계열교재

Footnotes

$\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#$↩︎
$\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#$↩︎
$\forall B \in {\cal S}: \mu(B)=\int_B f_X d\#$↩︎
분자, 분모에 들어가는 두개의 메져↩︎
카운팅메져인 $\#$↩︎
함수 $\#_X$은 확률변수 $X$의 support 에서만 값이 정의되는 카운팅메져라고 생각할 수 있음↩︎
조합에서도 성립하는지 보기 위해서↩︎
디렉메져에 항상 0 포함하니까 1이 될 것↩︎
msr의 정의에 따라 두 값은 양수↩︎
즉 각각이 0이 나온다.↩︎
$\lambda(B) = 0$이어서 0↩︎
$\delta_0(B) = 0$이어서 0↩︎
$x$가 0일때 $\frac{1}{2}$이 되고 다 0임.↩︎
르벡적분할떄는 $x=0$ 안 봐도 되니까 $\frac{1}{2}\le x \le1$만 신경쓰기↩︎
증가함수↩︎
칸토어처럼 이상한 연속함수 말고 상식적인 수준의 연속함수라는 의미↩︎
이렇게 정의해도 되는 이유는 카라테오도리 확장정리덕분↩︎
${\cal R} \cap [0,2\pi) := \{B \cap [0,2\pi): B \in {\cal R}\}$↩︎
이렇게 정의해도 되는 이유는 카라테오도리 확장정리덕분↩︎