df_4 = data.frame(x = c(0,0,3,3,6,6,9,9,12,12),
y = c(8.5,8.4,7.9,8.1,7.8,7.6,7.3,7.0,6.8,6.7))
df_4| x | y |
|---|---|
| <dbl> | <dbl> |
| 0 | 8.5 |
| 0 | 8.4 |
| 3 | 7.9 |
| 3 | 8.1 |
| 6 | 7.8 |
| 6 | 7.6 |
| 9 | 7.3 |
| 9 | 7.0 |
| 12 | 6.8 |
| 12 | 6.7 |
고급회귀분석 과제, CH03,04,05
고급회귀분석 두번째 과제입니다.
제출 기한 : 10월 23일
(마지막 문제는 R을 이용해서 풀이해도 됨)
제출 방법
직접 제출(607호) 도 가능하지만,
문서 작성 후 pdf로 변환(★★★)하여 lms에 제출을 추천
(pdf 아닌 문서는 미제출로 간주)
주의사항
pdf로 꼭 변환하여 제출
풀이가 꼭 있어야 함 (답만 적혀 있는 경우 ’0’점 처리)
부정행위 시 ’F’학점
계산은 R로 해도 되지만 계산 풀이 과정이 꼭 있어야 함!!
예) R에서 lm으로 beta의 추정량을 구하면 안 됨. 수업 시간에 배운 식으로 풀이를 적어야 함.
************ R을 이용해서 푸는 문제는, R 코드도 같이 업로드.
1.
단순회귀에서 회귀제곱합, \[SSE = \sum^{n}_{i=1} (y_i - \hat{y}_i)^2\] 을 이차형식 \(y^\top B y\) 로 표현하시오. 이 이차형식의 분포를 구하고, 또한 기대치를 ⟨정리 5.1⟩에 의하여 구하시오
Answer
\(\sum^{n}_{i=1} (y_i - \hat{y}_i)^2\)
\(= \sum^{n}_{i=1} (y_i - \hat{y}_i)^\top(y_i - \hat{y}_i)\)
\(= (\bf{y} - \hat{\bf{y}})^\top(\bf{y} - \hat{\bf{y}})\)
\(= (\bf{y} - \bf{X}b)^\top(\bf{y} - \bf{X}b)\)
\(= \bf{y}^\top\bf{y} - \bf{y}^\top X\bf{b} - \bf{b}^\top\bf{X}^\top\bf{y} + \bf{b}^\top\bf{X}^\top\bf{X}\bf{b}\)
\(= \bf{y}^\top\bf{y} - 2\bf{y}^\top\bf{X}\bf{b} + \bf{b}^\top\bf{X}^\top\bf{X}\bf{b}\)
\(= \bf{y}^\top\bf{y} - \bf{y}^\top\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top\bf{y}\)
\(= \bf{y}^\top(\bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\bf{y}\)
\(\frac{\sum^{n}_{i=1} (y_i - \hat{y}_i)^2}{\sigma^2} = \bf{y}^\top \bf{B} \bf{y}\)
<정리5.3>
만약 \(y \sim N(\mu,V)\)이면,
\[y^\top A y \sim \chi^2 (r(A),\frac{1}{2}\mu^\top A \mu ) \to \text{AV : independent matrix}\]
\(\frac{SSE}{\sigma^2} = \bf{y}^\top\frac{1}{\sigma^2}(\bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\bf{y}\)
\(\frac{SSE}{\sigma^2} \sim \chi^2 (r(A),\frac{1}{2}\mu^\top A \mu )\)
\(\star y_i \sim N(\beta_0 + \beta_1 x_i, \sigma^2)\)
\(\star \bf{y}^\top \sim N(\mu, I\sigma^2)\)
\(\bf{B} = \bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top\)
\(\bf{B}\bf{B} = (\bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)(\bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\)
\(= \bf{I_n} - 2\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top + \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top = \bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top = \bf{B}\)
\(\therefore \bf{B} \text{ is an independendt matrix}\)
\(r(\bf{B}) = tr(\bf{B}) = tr(\bf{I_n} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top) = tr(\bf{I_n}) - tr(\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top) = n - (p+1)\)
\(V = I\sigma^2\)
\(\therefore \bf{BV = BVBV}\)
\(\therefore \bf{BV} \text{ is an independent matrix}\)
\(\mu^\top \bf{B} \mu = \mu^\top (\bf{I}-\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\mu = \beta^\top \bf{X}^\top (\bf{I} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\bf{X}\beta = \beta^\top \bf{X}^\top (\bf{X} - \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top\bf{X})\beta = 0\)
\(\star \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top\bf{X} = \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top \bf{X} = \bf{X}\)
\(\frac{SSE}{\sigma^2}\sim \chi^2_{(n-(p+1))}\)
<정리 5.1> 만약 \(y \sim N(\mu, V)\)이면, \[E(y^\top A y) = tr(AV) + \mu^\top A \mu, Cov(y,y^\top A y ) = 2 V A \mu\]
\(E(SSE) = tr(BV) + \mu^\top B \mu = tr(\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top V) + \mu^\top \bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top \mu = (n-(p+1))\sigma^2 + 0 = (n - (p+1))\sigma^2\)
\(Cov(y,y^\top B y) = 2VB\mu = 2 \sigma^2 (I-\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\mu = 2 \sigma^2 (I-\bf{X}(\bf{X}^\top\bf{X})^{-1}\bf{X}^\top)\bf{X}\beta = 0\)
2.
만약 \[y_1 = \beta_0 + \epsilon_1\] \[y_2 = 2\beta_0 - \beta_1 + \epsilon_2\] \[y_3 = \beta_0 + 2\beta_1 + \epsilon_3\] 이고, \(E(\epsilon_i) = 0, i = 1, 2, 3\)이라면 \(\beta_0\) 와 \(\beta_1\) 의 최소제곱추정값은 무엇인가? \(y_i, i = 1, 2, 3\)의 함수로써 나타내어라. 그리고 이 경우의 잔차제곱합(residual sum of squares)을 구하시오.
Answer
\(\epsilon_1 = y_1 + \beta_0, \epsilon_2 = y_2 - 2\beta_0 + \beta_1, \epsilon_3 = y_3 - \beta_0 - 2\beta_1\)
\(S = (y_1 - \hat{\beta}_0)^2 + (y_2 - 2\hat{\beta}_0 + \hat{\beta}_1)^2 + (y_3 - \hat{\beta}_0 - 2\hat{\beta}_1)^2\)
\(\frac{\partial S}{\partial \beta_0} = -2(y_1 - \hat{\beta}_0) -4(y_2 - 2\hat{\beta}_0 + \hat{\beta}_1) -2(y_3 - \hat{\beta}_0 - 2\hat{\beta}_1)\)
\(= -2y_1 + 2\hat{\beta}_0 -4y_2 + 8\hat{\beta}_0 -4\hat{\beta}_1 -2y_3 +2\hat{\beta}_0 +4\hat{\beta}_1\)
\(= -2y_1 -4y_2 -2y_3 + 12\hat{\beta}_0 = 0\)
\(\therefore \hat{\beta}_0 = \frac{1}{12}(2y_1 + 4y_2 + 2y_3) = \frac{1}{6}(y_1 + 2y_2 + y_3)\)
\(\frac{\partial S}{\partial \beta_1} = 2(y_2 - 2\hat{\beta}_0 + \hat{\beta}_1) -4(y_3 - \hat{\beta}_0 - 2\hat{\beta}_1)\)
\(= 2y_2 - 4\hat{\beta}_0 + 2\hat{\beta}_1 -4y_3 +4 \hat{\beta}_0 + 8\hat{\beta}_1\)
\(= 2y_2 -4y_3 + 10\hat{\beta}_1 = 0\)
\(\therefore \hat{\beta}_1 = \frac{1}{10}(-2y_2 + 4y_3) = \frac{1}{5}(-y_2 + 2y_3)\)
\(\text{Residual sum of squares }S = (y_1 - \hat{\beta}_0)^2 + (y_2 - 2\hat{\beta}_0 + \hat{\beta}_1)^2 + (y_3 - \hat{\beta}_0 - 2\hat{\beta}_1)^2\)
\(= y_2^2 + \hat{\beta}_0^2 - 2\hat{\beta}_0y_1 + y_2^2 - 4\hat{\beta}_0 y_2 + 2\hat{\beta}_1 y_2 - 4\hat{\beta}_0 \hat{\beta}_1 + \hat{\beta}_1^2 + y_3^2 -2\hat{\beta}_0 y_3 - 4 \hat{\beta}_1 y_3 + \hat{\beta}_0^2 + 4\hat{\beta}_0\hat{\beta}_ + 4\hat{\beta}_1^2\)
\(= y_1^2 + y_2^2 + y_3^2 + 2\hat{\beta}_0^2 + 5\hat{\beta}_1^2 + \hat{\beta}_0(-2y_1 -4y_2 -2y_3) + \hat{\beta}_1 (2y_2 -4y_3)\)
\(= y_1^2 + y_2^2 + y_3^2 -10 \hat{\beta}_0^2 - 5\hat{\beta}_1^2\)
\(= y_1^2 + y_2^2 + y_3^2 - \frac{5}{18}(y_1 + 2y_2 + y_3)^2 - \frac{1}{5}(-y_2 + 2y_3)^2\)
\(= \frac{13}{18} y_1^2 -\frac{14}{45}y_2^2 -\frac{70}{90}y3^2 -\frac{10}{9}y_1y_2 -\frac{5}{9} y_1y_3 - \frac{32}{45}y_2y_3\)
\(= \frac{1}{90}(65y_1^2 -28 y_2^2 - 70y_3^2 -100y_1y_2 -50y_1y_3 - 64y_2y_3)\)
3.
단순회귀모형 \[y_i = \beta_0 + \beta_1 x_i + \epsilon_i, \epsilon_i ~ N(0, \sigma^2), i = 1, 2, \dots , n\] 에서 각각의 \(x_i\) 가 \(cx_i (c \neq 0)\)로 대체된다고 가정하자. \(\hat{\beta}_0, \hat{\beta}_1, s^{2}_{y·x}, R^2\) 과 \(H_0 : \beta_1 = 0\)에 대한 \(t\)−검정 결과는 어떤 영향을 받는가?
Answer
\(S = \sum^n_{i=1}\epsilon^2_i = \sum^n_{i=1} \{ y_i - (\beta_0 + \beta_1 c x_i)\}^2\)
\(\frac{\partial S}{\partial \beta_1} = -2\sum^n_{i=1} c x_i (y_i - \hat{\beta}_0 - \hat{\beta}_1 c x_i) = \sum^n_{i=1} c x_i (y_i - \hat{y}) = \sum^n_{i=1} c x_i e_i = 0\)
\(= \sum^n_{i=1} c x_i (y_i - \hat{\beta}_0 - \hat{\beta}_1 c x_i ) =\sum^n_{i=1} c x_i (y_i - \bar{y} + \hat{\beta}_1 c\bar{x} - \hat{\beta}_1 c x_i) = \sum^n_{i=1} c x_i(y_i - \bar{y}) - \hat{\beta}_1 \sum^n_{i=1} c x_i (c x_i - c\bar{x})\)
\(\star \sum^n_{i=1} c x_i(y_i - \bar{y}) = \sum^n_{i=1}(c x_i - c\bar{x} + c\bar{x})(y_i - \bar{y}) = c\sum^n_{i=1}(x_i - \bar{x})(y_i - \bar{y}) + \sum^n_{i=1} c \bar{x}(y_i - \bar{y}) = c S_{xy}\)
\(\star \hat{\beta}_1 \sum^n_{i=1} c x_i (c x_i - c\bar{x}) = \hat{\beta}_1 \sum^n_{i=1} (c x_i - c \bar{x} + c \bar{x}) (c x_i - c \bar{x}) = \hat{\beta}_1 \{ \sum^n_{i=1} (c x_i - c \bar{x})(c x_i - c \bar{x}) + \sum^n_{i=1} c^2 \bar{x}( x_i - \bar{x}) \} = c^2 \hat{\beta}_1 S_{xx}\)
\(c S_{xy} - \hat{\beta}_1 c^2 S_{xx} = 0\)
\(\hat{\beta}_1 = \frac{S_{xy}}{c S_{xx}}\)
\(\hat{\beta}_1\) 은 \(\frac{1}{c}\)배가 되었다.
\(\frac{\partial S}{\partial \beta_0} = -2\sum^n_{i=1} (y_i - \hat{\beta}_0 - \hat{\beta}_1 c x_i) = \sum^n_{i=1} (y_i - \hat{y}_i) = \sum^n_{i=1}e_i = 0\)
\(n \hat{\beta}_0 = \sum^n_{i=1}y_i - \frac{1}{c} \hat{\beta}_1 c \sum^n_{i=1} x_i\)
\(\hat{\beta}_0 = \frac{1}{n} \sum^n_{i=1} y_i - \frac{1}{c}\hat{\beta}_1 c \frac{1}{n}\sum^n_{i=1} x_i = \bar{y} - \hat{\beta}_1 \bar{x}\)
\(\hat{\beta}_0\)은 \(x_i\)가 \(cx_i\)로 대체되었을때 영향을 받지 않았다.
\(S_{yx} = c \sum^n_{i=1}(x_i - \bar{x})(y_i - \bar{y})\)
\(S^2_{yx} = c^2 \sum^n_{i=1}(x_i - \bar{x})^2(y_i - \bar{y})^2\)
\(\star S_{xx} = c^2 \sum^n_{i=1} (x_i - \bar{x})(x_i - \bar{x})\)
\(\star S_{yy} = \sum^n_{i=1} (y_i - \bar{y})(y_i - \bar{y})\)
\(R^2 = r_{xy}^2 = \frac{S_{xy}^2}{S_{xx}S_{yy}} = \frac{c^2 \sum^n_{i=1}(x_i - \bar{x})^2(y_i - \bar{y})^2}{(c^2 \sum^n_{i=1} (x_i - \bar{x})(x_i - \bar{x}))(\sum^n_{i=1} (y_i - \bar{y})(y_i - \bar{y}))} = \frac{ \sum^n_{i=1}(x_i - \bar{x})^2(y_i - \bar{y})^2}{( \sum^n_{i=1} (x_i - \bar{x})(x_i - \bar{x}))(\sum^n_{i=1} (y_i - \bar{y})(y_i - \bar{y}))}\)
\(R^2\)은 영향을 받지 않았다.
회귀직선의 유의성 검정 \(H_0 : \beta_1 = 0 \text{ vs. } H_1: \beta_1 \neq 0\)
검정통계량 \(F = \frac{MSR}{MSE} = \frac{SSR/1}{SSE/(n-2)} \sim_{H_0} F(1,n-2)\)
검정통계량 계산에도 영향을 주지 않았기 때문에 \(\text{t test}\) 결과는 \(x_i\)에 \(c\)배를 한 후에도 같은 결과가 나온다.
4.
생선을 잡아서 얼음창고에 일주일 동안 보관한 후에 생선의 신선도가 어느 정도 변하는가를 실험하였다. 신선도를 \(y\)로 놓고 10점 만점으로 하여 0점이 신선도가 전혀 없는 것이고 10점이 가장 좋은 경우이다. 설명변수 \(x\)는 생선을 잡은 지 \(x\)시간이 경과한 후에 얼음창고에 넣는 것을 가리킨다. 실험으로 10개의 데이터를 얻었다.
| \(y\)(신선도) | 8.5 | 8.4 | 7.9 | 8.1 | 7.8 | 7.6 | 7.3 | 7.0 | 6.8 | 6.7 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x\)(경과시간) | 0 | 0 | 3 | 3 | 6 | 6 | 9 | 9 | 12 | 12 |
(1)
선형회귀모형 (\(y = \beta_0 + \beta_1 x + \epsilon\))이 타당한가를 유의수준 \(\alpha = 0.05\)를 사용하여 적합결여검정을 행하라.
Answer
\(H_0 : E(Y|X = x) = \beta_0 + \beta_1 x\)
\(H_1 : E(Y|X=x) \neq \beta_0 + \beta_1 x\)
산점도
plot(df_4$x,df_4$y,xlab='x(경과시간)',ylab='y(신선도)')
우하향하는 모습이다.
df_4$x_barx = df_4$x - mean(df_4$x)
df_4$y_bary = df_4$y - mean(df_4$y) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_4$x_barx2 <- df_4$x_barx^2
df_4$y_bary2 <- df_4$y_bary^2
df_4$xy <-df_4$x_barx * df_4$y_bary- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_4| x | y | x_barx | y_bary | x_barx2 | y_bary2 | xy |
|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 0 | 8.5 | -6 | 0.89 | 36 | 0.7921 | -5.34 |
| 0 | 8.4 | -6 | 0.79 | 36 | 0.6241 | -4.74 |
| 3 | 7.9 | -3 | 0.29 | 9 | 0.0841 | -0.87 |
| 3 | 8.1 | -3 | 0.49 | 9 | 0.2401 | -1.47 |
| 6 | 7.8 | 0 | 0.19 | 0 | 0.0361 | 0.00 |
| 6 | 7.6 | 0 | -0.01 | 0 | 0.0001 | 0.00 |
| 9 | 7.3 | 3 | -0.31 | 9 | 0.0961 | -0.93 |
| 9 | 7.0 | 3 | -0.61 | 9 | 0.3721 | -1.83 |
| 12 | 6.8 | 6 | -0.81 | 36 | 0.6561 | -4.86 |
| 12 | 6.7 | 6 | -0.91 | 36 | 0.8281 | -5.46 |
round(colSums(df_4),3)- x
- 60
- y
- 76.1
- x_barx
- 0
- y_bary
- 0
- x_barx2
- 180
- y_bary2
- 3.729
- xy
- -25.5
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_4 <- as.numeric(colSums(df_4)[7]/colSums(df_4)[5])
beta0_4 <- mean(df_4$y) - beta1_4 * mean(df_4$x)cat("hat beta0 = ", beta0_4)
cat("\nhat beta1 = ", beta1_4)hat beta0 = 8.46
hat beta1 = -0.1416667\(\hat{y} = 8.46 - 0.1417x\)
SST_4 = sum((df_4$y - mean(df_4$y))^2)SSR_4 = sum( ( ( beta0_4 + beta1_4 *df_4$x)-mean(df_4$y) )^2 )
MSR_4 = SSR_4/1SSE_4 = sum( ( df_4$y-( beta0_4 + beta1_4 *df_4$x))^2 )
MSE_4 = SSE_4/8cat("SST = ", SST_4,", df = 9")
cat("\nSSR = ", SSR_4,", df = 1")
cat("\nSSE = ", SSE_4, ", df = 8")SST = 3.729 , df = 9
SSR = 3.6125 , df = 1
SSE = 0.1165 , df = 8F_4 = MSR_4 / MSE_4
F_4
248.068669527898
qf(0.95,1,8)
5.31765507157871
\(H_0 : \beta_1 = 0\)
\(H_1 : \beta_1 \neq 0\)
F값이 유의수준 0.05에서 기준 F보다 크기 때문에 \(H_0\) 기각하고, \(\beta_1\) 은 유의미하다.
df_4_ex <- cbind(df_4[c(1,3,5,7,9),c(1,2)],df_4[c(2,4,6,8,10),c(2)])colnames(df_4_ex) <- c('x','y1','y2')df_4_ex$ymean <- (df_4_ex$y1+df_4_ex$y2)/2
df_4_ex$y1_ymean2 <- (df_4_ex$y1 - df_4_ex$ymean)^2
df_4_ex$y2_ymean2 <- (df_4_ex$y2 - df_4_ex$ymean)^2
df_4_ex$yhat <- 8.46 - 0.146667 * df_4_ex$x
df_4_ex| x | y1 | y2 | ymean | y1_ymean2 | y2_ymean2 | yhat | |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 0 | 8.5 | 8.4 | 8.45 | 0.0025 | 0.0025 | 8.460000 |
| 3 | 3 | 7.9 | 8.1 | 8.00 | 0.0100 | 0.0100 | 8.019999 |
| 5 | 6 | 7.8 | 7.6 | 7.70 | 0.0100 | 0.0100 | 7.579998 |
| 7 | 9 | 7.3 | 7.0 | 7.15 | 0.0225 | 0.0225 | 7.139997 |
| 9 | 12 | 6.8 | 6.7 | 6.75 | 0.0025 | 0.0025 | 6.699996 |
\(\hat{y} = 8.46 - 01417x\)
SSPE_4 = sum(df_4_ex$y1_ymean2) + sum(df_4_ex$y2_ymean2)
SSPE_4
0.0949999999999998
SSLF_4 = SSE_4 - SSPE_4
SSLF_4
0.0214999999999996
F_4_0 = SSLF_4/3 / (SSPE_4 / 5)
F_4_0
0.377192982456135
cat("유의수준 5%에서 ",qf(0.95,3,5), "보다 ",F_4_0,"값이 작기 때문에 귀무가설을 기각하지 못한다. 따라서 선형회귀모형은 타당하다.")유의수준 5%에서 5.409451 보다 0.377193 값이 작기 때문에 귀무가설을 기각하지 못한다. 따라서 선형회귀모형은 타당하다.\(H_0 : E(Y|X = x) = \beta_0 + \beta_1 x\) 기각못함
(2)
선형회귀모형이 타당한 경우, 신선도의 점수가 시간당 얼마만큼이나 떨어지는가를 95% 신뢰계수를 가지고 구간추정하라(즉, \(\beta_1\)의 구간추정).
Answer
\(\hat{\beta}_1\)의 \(100(1-\alpha)\)%의 신뢰구간
\(\hat{\beta}_1 \pm t_{\alpha/2}(n-2)\frac{\sqrt{MSE}}{\sqrt{S_{xx}}}\)
qt(0.975,8)
2.30600413520417
cat("beta1 is ",beta1_4)
cat("\nMSE is ",MSE_4)
cat("\nSxx is ",sum(df_4$x_barx2))beta1 is -0.1416667
MSE is 0.0145625
Sxx is 180cat("95% 신뢰계수는 (",beta1_4-qt(0.975,8)*sqrt(MSE_4/sum(df_4$x_barx2)),"-",beta1_4+qt(0.975,8)*sqrt(MSE_4/sum(df_4$x_barx2)),") 이다.")95% 신뢰계수는 ( -0.1624082 - -0.1209251 ) 이다.신뢰계수가 0을 포함하지 않는다. 신뢰구간에서 \(\beta_1\)이 유의미함을 알 수 있다.
- 두 타이어회사 A, B에서 생산되는 타이어를 비교하기 위하여 고속도로에서 트럭이 달리는 상황을 모의실험(simulated experiment)하여 다음의 데이터를 얻었다. \(x\)는 트럭이 달리는 속도이고 \(y\)는 타이어가 마모되기까지의 총 주행거리이다.
| \(x_{1j}\) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
|---|---|---|---|---|---|---|---|
| \(y_{1j}(A)\) | 9.8 | 12.5 | 14.9 | 16.5 | 22.4 | 24.1 | 25.8 |
| \(y_{2j}(B)\) | 15.0 | 14.5 | 16.5 | 19.1 | 22.3 | 20.8 | 22.4 |
- 산점도를 그리시오.
Answer
df_5 = data.frame(x = c(10,20,30,40,50,60,70),
yA = c(9.8,12.5,14.9,16.5,22.4,24.1,25.8),
yB = c(15.0,14.5,16.5,19.1,22.3,20.8,22.4))
df_5| x | yA | yB |
|---|---|---|
| <dbl> | <dbl> | <dbl> |
| 10 | 9.8 | 15.0 |
| 20 | 12.5 | 14.5 |
| 30 | 14.9 | 16.5 |
| 40 | 16.5 | 19.1 |
| 50 | 22.4 | 22.3 |
| 60 | 24.1 | 20.8 |
| 70 | 25.8 | 22.4 |
plot(df_5$yA~df_5$x,
xlab = "x",
ylab = "yA(orange),yB(blue)",
pch = 16,
cex = 1,
col = "darkorange")
par(new=TRUE)
plot(df_5$yB~df_5$x,
xlab='',
ylab='',
pch = 16,
cex = 1,
col = "blue")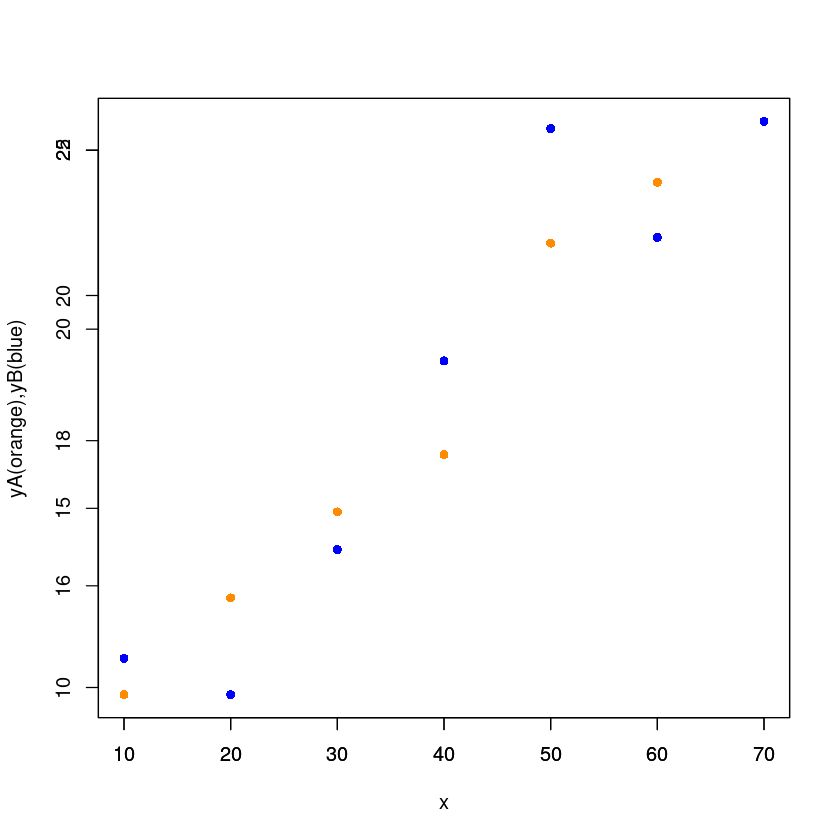
- 각 회사별로 속도와 총주행거리 간의 회귀모형을 구한다면, 두 개의 직선이 동일하다고 볼수 있는가? 유의수준 \(\alpha = 0.05\)로 가설검정하시오.
Answer
\(H_0: \beta_{01} = \beta_{02} \text{ and } \beta_{11} = \beta_{12}\)
\(H_1: \beta_{01} \ne \beta_{02} \text{ or } \beta_{11} \ne \beta_{12}\)
df_5_A <- df_5df_5_A$x_barx = df_5_A$x - mean(df_5_A$x)
df_5_A$yA_baryA = df_5_A$yA - mean(df_5_A$yA) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_5_A$x_barx2 <- df_5_A$x_barx^2
df_5_A$yA_baryA2 <- df_5_A$yA_baryA^2
df_5_A$xyA <-df_5_A$x_barx * df_5_A$yA_baryA- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_5_A| x | yA | yB | x_barx | yA_baryA | x_barx2 | yA_baryA2 | xyA |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 10 | 9.8 | 15.0 | -30 | -8.2 | 900 | 67.24 | 246 |
| 20 | 12.5 | 14.5 | -20 | -5.5 | 400 | 30.25 | 110 |
| 30 | 14.9 | 16.5 | -10 | -3.1 | 100 | 9.61 | 31 |
| 40 | 16.5 | 19.1 | 0 | -1.5 | 0 | 2.25 | 0 |
| 50 | 22.4 | 22.3 | 10 | 4.4 | 100 | 19.36 | 44 |
| 60 | 24.1 | 20.8 | 20 | 6.1 | 400 | 37.21 | 122 |
| 70 | 25.8 | 22.4 | 30 | 7.8 | 900 | 60.84 | 234 |
round(colSums(df_5_A),3)- x
- 280
- yA
- 126
- yB
- 130.6
- x_barx
- 0
- yA_baryA
- 0
- x_barx2
- 2800
- yA_baryA2
- 226.76
- xyA
- 787
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_xyA <- as.numeric(colSums(df_5_A)[8]/colSums(df_5_A)[6])
beta0_xyA <- mean(df_5_A$yA) - beta1_xyA * mean(df_5_A$x)cat("xyA hat beta0 = ", beta0_xyA)
cat("\nxyA hat beta1 = ", beta1_xyA)xyA hat beta0 = 6.757143
xyA hat beta1 = 0.2810714\(yA = 6.757143 + 0.2810714x\)
SST_A = sum((df_5_A$yA - mean(df_5_A$yA))^2)SSR_A = sum( ( ( 6.757143 + 0.2810714 *df_5_A$x)-mean(df_5_A$yA) )^2 )SSE_A = sum( ( df_5_A$yA-( 6.757143 + 0.2810714 *df_5_A$x))^2 )cat("yA SST = ", SST_A,", df = 6")
cat("\nyA SSR = ", SSR_A,", df = 1")
cat("\nyA SSE = ", SSE_A, ", df = 5")yA SST = 226.76 , df = 6
yA SSR = 221.2032 , df = 1
yA SSE = 5.556786 , df = 5df_5_B <- df_5df_5_B$x_barx = df_5_B$x - mean(df_5_B$x)
df_5_B$yB_baryB = df_5_B$yB - mean(df_5_B$yB) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_5_B$x_barx2 <- df_5_B$x_barx^2
df_5_B$yB_baryB2 <- df_5_B$yB_baryB^2
df_5_B$xyB <-df_5_B$x_barx * df_5_B$yB_baryB- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_5_B| x | yA | yB | x_barx | yB_baryB | x_barx2 | yB_baryB2 | xyB |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 10 | 9.8 | 15.0 | -30 | -3.6571429 | 900 | 13.3746939 | 109.71429 |
| 20 | 12.5 | 14.5 | -20 | -4.1571429 | 400 | 17.2818367 | 83.14286 |
| 30 | 14.9 | 16.5 | -10 | -2.1571429 | 100 | 4.6532653 | 21.57143 |
| 40 | 16.5 | 19.1 | 0 | 0.4428571 | 0 | 0.1961224 | 0.00000 |
| 50 | 22.4 | 22.3 | 10 | 3.6428571 | 100 | 13.2704082 | 36.42857 |
| 60 | 24.1 | 20.8 | 20 | 2.1428571 | 400 | 4.5918367 | 42.85714 |
| 70 | 25.8 | 22.4 | 30 | 3.7428571 | 900 | 14.0089796 | 112.28571 |
round(colSums(df_5_B),3)- x
- 280
- yA
- 126
- yB
- 130.6
- x_barx
- 0
- yB_baryB
- 0
- x_barx2
- 2800
- yB_baryB2
- 67.377
- xyB
- 406
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_xyB <- as.numeric(colSums(df_5_B)[8]/colSums(df_5_B)[6])
beta0_xyB <- mean(df_5_B$yB) - beta1_xyB * mean(df_5_B$x)cat("xyB hat beta0 = ", beta0_xyB)
cat("\nxyB hat beta1 = ", beta1_xyB)xyB hat beta0 = 12.85714
xyB hat beta1 = 0.145\(yB = 12.85714 + 0.145x\)
SST_B = sum((df_5_B$yB - mean(df_5_B$yB))^2)SSR_B = sum( ( ( 12.85714 + 0.145*df_5_B$x)-mean(df_5_B$yB) )^2 )SSE_B = sum( ( df_5_B$yB-( 12.85712 + 0.145 *df_5_B$x))^2 )cat("yB SST = ", SST_B,", df = 6")
cat("\nyB SSR = ", SSR_B,", df = 1")
cat("\nyB SSE = ", SSE_B, ", df = 5")yB SST = 67.37714 , df = 6
yB SSR = 58.87 , df = 1
yB SSE = 8.507143 , df = 5a <- df_5[,c(1,2)]colnames(a) <- c('x','y')b <- df_5[,c(1,3)]colnames(b) <- c('x','y')df_5_AB <- rbind(a,b)
df_5_AB| x | y |
|---|---|
| <dbl> | <dbl> |
| 10 | 9.8 |
| 20 | 12.5 |
| 30 | 14.9 |
| 40 | 16.5 |
| 50 | 22.4 |
| 60 | 24.1 |
| 70 | 25.8 |
| 10 | 15.0 |
| 20 | 14.5 |
| 30 | 16.5 |
| 40 | 19.1 |
| 50 | 22.3 |
| 60 | 20.8 |
| 70 | 22.4 |
df_5_AB$x_barx = df_5_AB$x - mean(df_5_AB$x)
df_5_AB$y_bary = df_5_AB$y - mean(df_5_AB$y) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_5_AB$x_barx2 <- df_5_AB$x_barx^2
df_5_AB$y_bary2 <- df_5_AB$y_bary^2
df_5_AB$xy <-df_5_AB$x_barx * df_5_AB$y_bary- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_5_AB| x | y | x_barx | y_bary | x_barx2 | y_bary2 | xy |
|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 10 | 9.8 | -30 | -8.5285714 | 900 | 72.736531 | 255.85714 |
| 20 | 12.5 | -20 | -5.8285714 | 400 | 33.972245 | 116.57143 |
| 30 | 14.9 | -10 | -3.4285714 | 100 | 11.755102 | 34.28571 |
| 40 | 16.5 | 0 | -1.8285714 | 0 | 3.343673 | 0.00000 |
| 50 | 22.4 | 10 | 4.0714286 | 100 | 16.576531 | 40.71429 |
| 60 | 24.1 | 20 | 5.7714286 | 400 | 33.309388 | 115.42857 |
| 70 | 25.8 | 30 | 7.4714286 | 900 | 55.822245 | 224.14286 |
| 10 | 15.0 | -30 | -3.3285714 | 900 | 11.079388 | 99.85714 |
| 20 | 14.5 | -20 | -3.8285714 | 400 | 14.657959 | 76.57143 |
| 30 | 16.5 | -10 | -1.8285714 | 100 | 3.343673 | 18.28571 |
| 40 | 19.1 | 0 | 0.7714286 | 0 | 0.595102 | 0.00000 |
| 50 | 22.3 | 10 | 3.9714286 | 100 | 15.772245 | 39.71429 |
| 60 | 20.8 | 20 | 2.4714286 | 400 | 6.107959 | 49.42857 |
| 70 | 22.4 | 30 | 4.0714286 | 900 | 16.576531 | 122.14286 |
round(colSums(df_5_AB),3)- x
- 560
- y
- 256.6
- x_barx
- 0
- y_bary
- 0
- x_barx2
- 5600
- y_bary2
- 295.649
- xy
- 1193
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_xy <- as.numeric(colSums(df_5_AB)[7]/colSums(df_5_AB)[5])
beta0_xy <- mean(df_5_AB$y) - beta1_xy * mean(df_5_AB$x)cat("xy hat beta0 = ", beta0_xy)
cat("\nxy hat beta1 = ", beta1_xy)xy hat beta0 = 9.807143
xy hat beta1 = 0.2130357\(\text{y} = 9.807143 +0.2130357\text{x}\)
SST_5 = sum((df_5_AB$y - mean(df_5_AB$y))^2)SSR_5 = sum( ( (9.807143 + 0.2130357*df_5_AB$x)-mean(df_5_AB$y) )^2 )SSE_5 = sum( ( df_5_AB$y-(9.807143 +0.2130357 *df_5_AB$x))^2 )cat("y = ",round(beta0_xy,4), "+ ",round(beta1_xy,4) ,"x")y = 9.8071 + 0.213 xcat("SST = ", SST_5,", df = 13")
cat("\nSSR = ", SSR_5,", df = 1")
cat("\nSSE = ", SSE_5, ", df = 12")SST = 295.6486 , df = 13
SSR = 254.1516 , df = 1
SSE = 41.49696 , df = 12cat("yA = ",round(beta0_xyA,4), "+ ",round(beta1_xyA,4) ,"x")yA = 6.7571 + 0.2811 xcat("yA SST = ", SST_A,", df = 6")
cat("\nyA SSR = ", SSR_A,", df = 1")
cat("\nyA SSE = ", SSE_A, ", df = 5")yA SST = 226.76 , df = 6
yA SSR = 221.2032 , df = 1
yA SSE = 5.556786 , df = 5cat("yB = ",round(beta0_xyB,4), "+ ",round(beta1_xyB,4) ,"x")yB = 12.8571 + 0.145 xcat("yB SST = ", SST_B,", df = 6")
cat("\nyB SSR = ", SSR_B,", df = 1")
cat("\nyB SSE = ", SSE_B, ", df = 5")yB SST = 67.37714 , df = 6
yB SSR = 58.87 , df = 1
yB SSE = 8.507143 , df = 5가설
\(H_0 : \beta_{01} = \beta_{02} \text{ and } \beta_{11} = \beta_{12}\)
\(H_1 : \beta_{01} \neq \beta_{02} \text{ or } \beta_{11} \neq \beta_{12}\)
검정통계량
\(F_0 = \frac{SSE(R) - SSE(F)}{df_R-df_F} \times \frac{df_F}{SSE(F)}\)
SSE_5_F = SSE_A + SSE_B
df_5_F = 5 -2 + 5 -2SSE_5_R = SSE_5
df_5_R = 5 -1 + 5 -1F_5_0 = (SSE_5_R - SSE_5_F)/(df_5_R - df_5_F) / (SSE_5_F/df_5_F)
F_5_0
5.8517864828756
df_5_R - df_5_F
2
df_5_F
6
F_5_stan = qf(0.95,2,10)
F_5_stan
4.1028210151304
cat(F_5_0, " 는 유의수준 0.05에서 F값 ", F_5_stan , " 보다 크다.")
cat("\n따라서 귀무가설을 기각하였고, 두 회귀모형은 beta0가 다르거나")
cat("\n혹은 beta1이 다르거나 혹은 beta0,beta1 모두가 다르다.")5.851786 는 유의수준 0.05에서 F값 4.102821 보다 크다.
따라서 귀무가설을 기각하였고, 두 회귀모형은 beta0가 다르거나
혹은 beta1이 다르거나 혹은 beta0,beta1 모두가 다르다.\(H_0 : \beta_{01} = \beta_{02} \text{ and } \beta_{11} = \beta_{12}\) 기각
(3)
관심의 대상이 \(x\)가 증가함에 따라 \(y\) 가 얼마나 증가하는가에 있다. 두 회사의 타이어에 대하여 각각 회귀모형을 적합했을 때, 기울기가 같은지 유의수준 5%로 검정하시오.
Answer
기울기 비교에 대한 가설
\(H_0 : \beta_{11} = \beta_{12} \text{ vs. } H_1 : \beta_{11} \neq \beta_{12}\)
검정통계량
\(t_0 = \frac{ \hat{\beta}_{11} - \hat{\beta}_{12} }{ \sqrt{ \hat{Var}( \hat{\beta}_{11} - \hat{\beta}_{12} ) } }\)
\(\text{Degree of Freedom} = t((n_1 - 1) + (n_2 - 1))\)
\(\hat{Var}( \hat{\beta}_{11} - \hat{\beta}_{12} ) = MSE(F) [\frac{1}{\sum(x_{1j} - \bar{x}_1)^2} + \frac{1}{\sum(x_{2j} - \bar{x}_2)^2}]\)
round(beta1_xyA,4)
0.2811
round(beta1_xyB,4)
0.145
SSE_5_F
14.063928575095
MSE_5_F = SSE_5_F / df_5_F
MSE_5_F
2.34398809584917
sum(df_5_A$x_barx2)
2800
sum(df_5_B$x_barx2)
2800
var_5_diff = MSE_5_F * (1/sum(df_5_A$x_barx2) + 1/sum(df_5_B$x_barx2))
var_5_diff
0.00167427721132084
t_5_0 = (beta1_xyA - beta1_xyB)/sqrt(var_5_diff)
t_5_0
3.32547173820247
qt(0.95,df_5_F)
1.9431802805153
cat(t_5_0,"는 ",qt(0.95,df_5_F),"보다 크다. 따라서 유의수준 5%에서 귀무가설을 기각하여 두 회귀모형의 기울기가 다르다고 할 수 있다.")3.325472 는 1.94318 보다 크다. 따라서 유의수준 5%에서 귀무가설을 기각하여 두 회귀모형의 기울기가 다르다고 할 수 있다.\(H_0 : \beta_{11} = \beta_{12}\) 기각
6.
R 실습. 아마존 강 수위 문제 아마존 강 유역은 지구상의 가장 큰 열대림 지역이지만 대부분의 다른 자연자원과 마찬가지로 개발의 손길이 미치면서 열대림이 급속히 파괴됐다. 1970년대 이후 아마존 상류지역에 도로가 건설되면서 인구가 빠르게 증가되었고 대규모의 삼림파괴가 이뤄졌다. 강수량과 유수량이 모두 영향을 받을 수 있기 때문에 이것은 결국 아마존 강 전체에 영향을 미치는 심각한 기후학적 및 수문학적 변화를 가져왔다. 다음의 표는 페루 이키토스(Iquitos)에서 1962년부터 1978년까지 기록한 아마존 강 최고수위 (High)와, 최저수위 (Low)를 기록한 것이다(단위: 미터).1962년부터 1969년까지의 데이터는 개발 이전에 수집된 데이터이고, 1970년부터 1978년까지의 데이터는 개발이후에 관측된 데이터를 나타낸다. 이 데이터는 아마존 상류지역의 삼림파괴가 아마존 유역의 강 수위에 변화를 일으켰는지 분석하고자 한다. 우리의 관심은 시간에 따른 아마존 강 수위 변화여부이다. 예를 들어, 우리가 다음을 적합한다면
\[\text{High} = \beta_0 + \beta_1 \times \text{Year} + \epsilon\]
\(\beta_1 = 0\)은 시간에 따른 아마존 강의 최고수위에 아무런 (선형)변화가 없다는 것을 의미하고,
\(\beta_1 > 0\)은 아마존 강의 최고수위가 증가된 것을 의미하는데, 이것은 해마다 아마존 강의 흐르는 물이 늘어난 것을 나타낼 수 있다.
\(\beta_1 < 0\)은 시간에 따라 아마존 강의 최고수위가 낮아진 것을 의미하는데, 이것은 해마다 아마존 강의 흐르는 물이 줄어든 것을 의미한다. 다음의 물음에 답하시오.
\[\text{Table 1: 아마존 강 데이터 (Amazon River data)}\]
| Year | High(m) | Low(m) |
|---|---|---|
| 1962 | 25.82 | 18.24 |
| 1963 | 25.35 | 16.50 |
| 1964 | 24.29 | 20.26 |
| 1965 | 24.05 | 20.97 |
| 1966 | 24.89 | 19.43 |
| 1967 | 25.35 | 19.31 |
| 1968 | 25.23 | 20.85 |
| 1969 | 25.06 | 19.54 |
| 1970 | 27.13 | 20.49 |
| 1971 | 27.36 | 21.91 |
| 1972 | 26.65 | 22.51 |
| 1973 | 27.13 | 18.81 |
| 1974 | 27.49 | 19.42 |
| 1975 | 27.08 | 19.10 |
| 1976 | 27.51 | 18.80 |
| 1977 | 27.54 | 18.80 |
| 1978 | 26.21 | 17.57 |
(1)
High와 Year, Low와 Year, 그리고 High와 Low에 대해 산점도를 그리시오.
Answer
df_6 = data.frame(Year = c(1962,1963,1964,1965,1966,1967,1968,1969,1970,1971,1972,1973,1974,1975,1976,1977,1978),
High = c(25.82, 25.35, 24.29, 24.05, 24.89, 25.35, 25.23, 25.06, 27.13, 27.36, 26.65, 27.13, 27.49, 27.08, 27.51, 27.54, 26.21),
Low = c(18.24, 16.50, 20.26, 20.97, 19.43, 19.31, 20.85, 19.54, 20.49, 21.91, 22.51, 18.81, 19.42, 19.10, 18.80, 18.80, 17.57))
df_6| Year | High | Low |
|---|---|---|
| <dbl> | <dbl> | <dbl> |
| 1962 | 25.82 | 18.24 |
| 1963 | 25.35 | 16.50 |
| 1964 | 24.29 | 20.26 |
| 1965 | 24.05 | 20.97 |
| 1966 | 24.89 | 19.43 |
| 1967 | 25.35 | 19.31 |
| 1968 | 25.23 | 20.85 |
| 1969 | 25.06 | 19.54 |
| 1970 | 27.13 | 20.49 |
| 1971 | 27.36 | 21.91 |
| 1972 | 26.65 | 22.51 |
| 1973 | 27.13 | 18.81 |
| 1974 | 27.49 | 19.42 |
| 1975 | 27.08 | 19.10 |
| 1976 | 27.51 | 18.80 |
| 1977 | 27.54 | 18.80 |
| 1978 | 26.21 | 17.57 |
plot(df_6$High,df_6$Year,
xlab = "Year",
ylab = "High",
pch = 16,
cex = 1)
양의 기울기로 선형 관계를 갖는 모습이다.
plot(df_6$Low~df_6$Year,
xlab = "Year",
ylab = "Low",
pch = 16,
cex = 1)
이차함수 모양의 연관이 있는 모양새이다.
plot(df_6$Low~df_6$High,
xlab = "Low",
ylab = "High",
pch = 16,
cex = 1)
관련이 있는지 모르겠다.
(2)
Year에 대한 High, Year에 대한 Low, 그리고 Low에 대한 High의 회귀모형을 구하시오. 3개 회귀모형의 결과를 요약하고, 각 모형별로 회귀계수의 의미를 설명하시오.
Answer
Year에 대한 High의 회귀모형
df_6_YearHigh <- df_6df_6_YearHigh$Year_barYear = df_6_YearHigh$Year - mean(df_6_YearHigh$Year)
df_6_YearHigh$High_barHigh = df_6_YearHigh$High - mean(df_6_YearHigh$High) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_6_YearHigh$Year_barYear2 <- df_6_YearHigh$Year_barYear^2
df_6_YearHigh$High_barHigh2 <- df_6_YearHigh$High_barHigh^2
df_6_YearHigh$YearHigh <-df_6_YearHigh$Year_barYear * df_6_YearHigh$High_barHigh- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_6_YearHigh| Year | High | Low | Year_barYear | High_barHigh | Year_barYear2 | High_barHigh2 | YearHigh |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 1962 | 25.82 | 18.24 | -8 | -0.30588235 | 64 | 0.093564014 | 2.4470588 |
| 1963 | 25.35 | 16.50 | -7 | -0.77588235 | 49 | 0.601993426 | 5.4311765 |
| 1964 | 24.29 | 20.26 | -6 | -1.83588235 | 36 | 3.370464014 | 11.0152941 |
| 1965 | 24.05 | 20.97 | -5 | -2.07588235 | 25 | 4.309287543 | 10.3794118 |
| 1966 | 24.89 | 19.43 | -4 | -1.23588235 | 16 | 1.527405190 | 4.9435294 |
| 1967 | 25.35 | 19.31 | -3 | -0.77588235 | 9 | 0.601993426 | 2.3276471 |
| 1968 | 25.23 | 20.85 | -2 | -0.89588235 | 4 | 0.802605190 | 1.7917647 |
| 1969 | 25.06 | 19.54 | -1 | -1.06588235 | 1 | 1.136105190 | 1.0658824 |
| 1970 | 27.13 | 20.49 | 0 | 1.00411765 | 0 | 1.008252249 | 0.0000000 |
| 1971 | 27.36 | 21.91 | 1 | 1.23411765 | 1 | 1.523046367 | 1.2341176 |
| 1972 | 26.65 | 22.51 | 2 | 0.52411765 | 4 | 0.274699308 | 1.0482353 |
| 1973 | 27.13 | 18.81 | 3 | 1.00411765 | 9 | 1.008252249 | 3.0123529 |
| 1974 | 27.49 | 19.42 | 4 | 1.36411765 | 16 | 1.860816955 | 5.4564706 |
| 1975 | 27.08 | 19.10 | 5 | 0.95411765 | 25 | 0.910340484 | 4.7705882 |
| 1976 | 27.51 | 18.80 | 6 | 1.38411765 | 36 | 1.915781661 | 8.3047059 |
| 1977 | 27.54 | 18.80 | 7 | 1.41411765 | 49 | 1.999728720 | 9.8988235 |
| 1978 | 26.21 | 17.57 | 8 | 0.08411765 | 64 | 0.007075779 | 0.6729412 |
round(colSums(df_6_YearHigh),3)- Year
- 33490
- High
- 444.14
- Low
- 332.51
- Year_barYear
- 0
- High_barHigh
- 0
- Year_barYear2
- 408
- High_barHigh2
- 22.951
- YearHigh
- 73.8
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_YearHigh <- as.numeric(colSums(df_6_YearHigh)[8]/colSums(df_6_YearHigh)[6])
beta0_YearHigh <- mean(df_6_YearHigh$High) - beta1_YearHigh * mean(df_6_YearHigh$Year)cat("YearHigh hat beta0 = ", beta0_YearHigh)
cat("\nYearHigh hat beta1 = ", beta1_YearHigh)YearHigh hat beta0 = -330.2124
YearHigh hat beta1 = 0.1808824\(\text{High} = -330.21235 + 0.18088\text{Year}\)
R결과와 비교
summary(lm(df_6$High~df_6$Year))
Call:
lm(formula = df_6$High ~ df_6$Year)
Residuals:
Min 1Q Median 3Q Max
-1.3629 -0.5341 0.1479 0.4903 1.1412
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -330.21235 78.03319 -4.232 0.000725 ***
df_6$Year 0.18088 0.03961 4.567 0.000371 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8001 on 15 degrees of freedom
Multiple R-squared: 0.5816, Adjusted R-squared: 0.5537
F-statistic: 20.85 on 1 and 15 DF, p-value: 0.0003708R결과 해석 - beta0과 beta1이 5%보다 유의확률이 작아 유의미하다. - 모형의 설명력은 50%정도에 머문다. - 모형의 p값이 0.05보다 작아 유의미하다고 볼 수 있다.
Year에 대한 Low의 회귀모형
df_6_YearLow <- df_6df_6_YearLow$Year_barYear = df_6_YearLow$Year - mean(df_6_YearLow$Year)
df_6_YearLow$Low_barLow = df_6_YearLow$Low - mean(df_6_YearLow$Low) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_6_YearLow$Year_barYear2 <- df_6_YearLow$Year_barYear^2
df_6_YearLow$Low_barLow2 <- df_6_YearLow$Low_barLow^2
df_6_YearLow$YearLow <-df_6_YearLow$Year_barYear * df_6_YearLow$Low_barLow- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_6_YearLow| Year | High | Low | Year_barYear | Low_barLow | Year_barYear2 | Low_barLow2 | YearLow |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 1962 | 25.82 | 18.24 | -8 | -1.31941176 | 64 | 1.7408474048 | 10.55529412 |
| 1963 | 25.35 | 16.50 | -7 | -3.05941176 | 49 | 9.3600003460 | 21.41588235 |
| 1964 | 24.29 | 20.26 | -6 | 0.70058824 | 36 | 0.4908238754 | -4.20352941 |
| 1965 | 24.05 | 20.97 | -5 | 1.41058824 | 25 | 1.9897591696 | -7.05294118 |
| 1966 | 24.89 | 19.43 | -4 | -0.12941176 | 16 | 0.0167474048 | 0.51764706 |
| 1967 | 25.35 | 19.31 | -3 | -0.24941176 | 9 | 0.0622062284 | 0.74823529 |
| 1968 | 25.23 | 20.85 | -2 | 1.29058824 | 4 | 1.6656179931 | -2.58117647 |
| 1969 | 25.06 | 19.54 | -1 | -0.01941176 | 1 | 0.0003768166 | 0.01941176 |
| 1970 | 27.13 | 20.49 | 0 | 0.93058824 | 0 | 0.8659944637 | 0.00000000 |
| 1971 | 27.36 | 21.91 | 1 | 2.35058824 | 1 | 5.5252650519 | 2.35058824 |
| 1972 | 26.65 | 22.51 | 2 | 2.95058824 | 4 | 8.7059709343 | 5.90117647 |
| 1973 | 27.13 | 18.81 | 3 | -0.74941176 | 9 | 0.5616179931 | -2.24823529 |
| 1974 | 27.49 | 19.42 | 4 | -0.13941176 | 16 | 0.0194356401 | -0.55764706 |
| 1975 | 27.08 | 19.10 | 5 | -0.45941176 | 25 | 0.2110591696 | -2.29705882 |
| 1976 | 27.51 | 18.80 | 6 | -0.75941176 | 36 | 0.5767062284 | -4.55647059 |
| 1977 | 27.54 | 18.80 | 7 | -0.75941176 | 49 | 0.5767062284 | -5.31588235 |
| 1978 | 26.21 | 17.57 | 8 | -1.98941176 | 64 | 3.9577591696 | -15.91529412 |
round(colSums(df_6_YearLow),3)- Year
- 33490
- High
- 444.14
- Low
- 332.51
- Year_barYear
- 0
- Low_barLow
- 0
- Year_barYear2
- 408
- Low_barLow2
- 36.327
- YearLow
- -3.22
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_YearLow <- as.numeric(colSums(df_6_YearLow)[8]/colSums(df_6_YearLow)[6])
beta0_YearLow <- mean(df_6_YearLow$Low) - beta1_YearLow * mean(df_6_YearLow$Year)cat("YearLow hat beta0 = ", beta0_YearLow)
cat("\nYearLow hat beta1 = ", beta1_YearLow)YearLow hat beta0 = 35.10696
YearLow hat beta1 = -0.007892157\(\text{Low} = 35.106961 -0.007892\text{Year}\)
R결과와 비교
summary(lm(df_6$Low~df_6$Year))
Call:
lm(formula = df_6$Low ~ df_6$Year)
Residuals:
Min 1Q Median 3Q Max
-3.1147 -0.7121 -0.1610 0.9306 2.9664
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.106961 151.723912 0.231 0.82
df_6$Year -0.007892 0.077017 -0.102 0.92
Residual standard error: 1.556 on 15 degrees of freedom
Multiple R-squared: 0.0006996, Adjusted R-squared: -0.06592
F-statistic: 0.0105 on 1 and 15 DF, p-value: 0.9197R결과 해석 - beta0과 beta1이 5%보다 유의확률이 커 유의미하지 않다. - 모형의 설명력은 굉장히 낮았다. - 모형의 p값이 0.05보다 커 유의미하지 않다.
Low에 대한 High의 회귀모형
df_6_LowHigh <- df_6df_6_LowHigh$Low_barLow = df_6_LowHigh$Low - mean(df_6_LowHigh$Low)
df_6_LowHigh$High_barHigh = df_6_LowHigh$High - mean(df_6_LowHigh$High) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_6_LowHigh$Low_barLow2 <- df_6_LowHigh$Low_barLow^2
df_6_LowHigh$High_barHigh2 <- df_6_LowHigh$High_barHigh^2
df_6_LowHigh$LowHigh <-df_6_LowHigh$Low_barLow * df_6_LowHigh$High_barHigh- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
df_6_LowHigh| Year | High | Low | Low_barLow | High_barHigh | Low_barLow2 | High_barHigh2 | LowHigh |
|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 1962 | 25.82 | 18.24 | -1.31941176 | -0.30588235 | 1.7408474048 | 0.093564014 | 0.40358478 |
| 1963 | 25.35 | 16.50 | -3.05941176 | -0.77588235 | 9.3600003460 | 0.601993426 | 2.37374360 |
| 1964 | 24.29 | 20.26 | 0.70058824 | -1.83588235 | 0.4908238754 | 3.370464014 | -1.28619758 |
| 1965 | 24.05 | 20.97 | 1.41058824 | -2.07588235 | 1.9897591696 | 4.309287543 | -2.92821522 |
| 1966 | 24.89 | 19.43 | -0.12941176 | -1.23588235 | 0.0167474048 | 1.527405190 | 0.15993772 |
| 1967 | 25.35 | 19.31 | -0.24941176 | -0.77588235 | 0.0622062284 | 0.601993426 | 0.19351419 |
| 1968 | 25.23 | 20.85 | 1.29058824 | -0.89588235 | 1.6656179931 | 0.802605190 | -1.15621522 |
| 1969 | 25.06 | 19.54 | -0.01941176 | -1.06588235 | 0.0003768166 | 1.136105190 | 0.02069066 |
| 1970 | 27.13 | 20.49 | 0.93058824 | 1.00411765 | 0.8659944637 | 1.008252249 | 0.93442007 |
| 1971 | 27.36 | 21.91 | 2.35058824 | 1.23411765 | 5.5252650519 | 1.523046367 | 2.90090242 |
| 1972 | 26.65 | 22.51 | 2.95058824 | 0.52411765 | 8.7059709343 | 0.274699308 | 1.54645536 |
| 1973 | 27.13 | 18.81 | -0.74941176 | 1.00411765 | 0.5616179931 | 1.008252249 | -0.75249758 |
| 1974 | 27.49 | 19.42 | -0.13941176 | 1.36411765 | 0.0194356401 | 1.860816955 | -0.19017405 |
| 1975 | 27.08 | 19.10 | -0.45941176 | 0.95411765 | 0.2110591696 | 0.910340484 | -0.43833287 |
| 1976 | 27.51 | 18.80 | -0.75941176 | 1.38411765 | 0.5767062284 | 1.915781661 | -1.05111522 |
| 1977 | 27.54 | 18.80 | -0.75941176 | 1.41411765 | 0.5767062284 | 1.999728720 | -1.07389758 |
| 1978 | 26.21 | 17.57 | -1.98941176 | 0.08411765 | 3.9577591696 | 0.007075779 | -0.16734464 |
round(colSums(df_6_LowHigh),3)- Year
- 33490
- High
- 444.14
- Low
- 332.51
- Low_barLow
- 0
- High_barHigh
- 0
- Low_barLow2
- 36.327
- High_barHigh2
- 22.951
- LowHigh
- -0.511
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
beta1_LowHigh <- as.numeric(colSums(df_6_LowHigh)[8]/colSums(df_6_LowHigh)[6])
beta0_LowHigh <- mean(df_6_LowHigh$High) - beta1_LowHigh * mean(df_6_LowHigh$Low)cat("LowHigh hat beta0 = ", beta0_LowHigh)
cat("\nLowHigh hat beta1 = ", beta1_LowHigh)LowHigh hat beta0 = 26.40088
LowHigh hat beta1 = -0.01405959\(\text{High} = 26.40088 -0.01406\text{Low}\)
R결과와 비교
summary(lm(df_6$Low~df_6$High))
Call:
lm(formula = df_6$Low ~ df_6$High)
Residuals:
Min 1Q Median 3Q Max
-3.0767 -0.7279 -0.1569 0.9529 2.9623
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.14079 8.49368 2.371 0.0315 *
df_6$High -0.02225 0.32478 -0.069 0.9463
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.556 on 15 degrees of freedom
Multiple R-squared: 0.0003129, Adjusted R-squared: -0.06633
F-statistic: 0.004695 on 1 and 15 DF, p-value: 0.9463R결과 해석 - beta0은 유의미 하지만 beta1이 5%보다 유의확률이 커 유의미하지 않다. - 모형의 설명력은 굉장히 낮았다. - 모형의 p값이 0.05보다 커 유의미하지 않다.
모형 정리
\(\text{Low} = 35.106961 -0.007892\text{Year}\) 모형의 의미 - \(\beta_0 = 35.106961\): 해당 모형에서 시간에 영향을 받지 않았을때의 아마존 강의 최저 수위가 35.106961m이다. - \(\beta_1 = -0.007892\): 아마존 강의 최저수위가 0.007892m만큼 감소한 것을 의미하는데, 이것은 해마다 아마존 강의 흐르는 물이 감소하는 것을 의미하지만, 0에 가까운 값으로서 영향이 미세해 보인다.
\(\text{High} = -330.21235 + 0.18088\text{Year}\) 모형의 의미 - \(\beta_0 = -330.21235\): 해당 모형에서 시간에 영향을 받지 않았을때의 아마존 강의 최고 수위가 -330.21235m이다. - \(\beta_1 = 0.18088\): 아마존 강의 최고수위가 0.18088m만큼 증가된 것을 의미하는데, 이것은 해마다 아마존 강의 흐르는 물이 0.18088m 늘어난 것을 나타낼 수 있다. 이 모형에서도 영향이 크게 끼치지 않는 것 같다.
\(\text{High} = 26.40088 -0.01406\text{Low}\) 모형의 의미 - \(\beta_0 = -26.40088\): 해당 모형에서 최저수위의 영향을 받지 않았을 때의 아마존 강의 최고수위가 026.40088m 라는 것을 의미한다. - \(\beta_1 = -0.014061\): 아마존 강의 최고수위가 최저수위가 1m 증가함에 따라 -0.0014061m 만큼 감소함을 의미한다. 아마존 강의 최저수위는 최고수위에 미치는 영향이 미미해 보인다.
(3)
이 자료를 근거로 우리는 삼림파괴가 아마존 강 수위의 변화를 일으킨다고 할 수 있는가?
Answer
- 1970년대 이후 삼림파괴가 이루어졌다. 구간을 나누어 보지 않는 이상 삼림파괴가 아마존 강 수위의 변화를 일으켰다는 판단은 섣불러 보인다.
- 모형만 봐도 시간과 아마존 강의 최고수위 및 최저수위의 영향과 아마존 강의 최저수위 및 최고수위 간의 영향이 거의 없어보인다. 모두 1도 넘지 않았기도 하다.
- 따라서 삼림파괴가 아마존 강 수위의 변화를 일으켰다고 2번의 근거로는 할 수 없다.
(4)
아마존강의 최저수위와 최고수위와의 산점도를 1960년대, 1970년대 자료별로 다르게 그리고, 각각의 회귀선을 적합하시오.
Answer
1960년대 아마존강의 최저수위와 최고수위와의 산점도
plot(df_6$High[df_6$Year<1970]~df_6$Low[df_6$Year<1970],
xlab = "Low",
ylab ="High",
pch = 16,
cex = 1)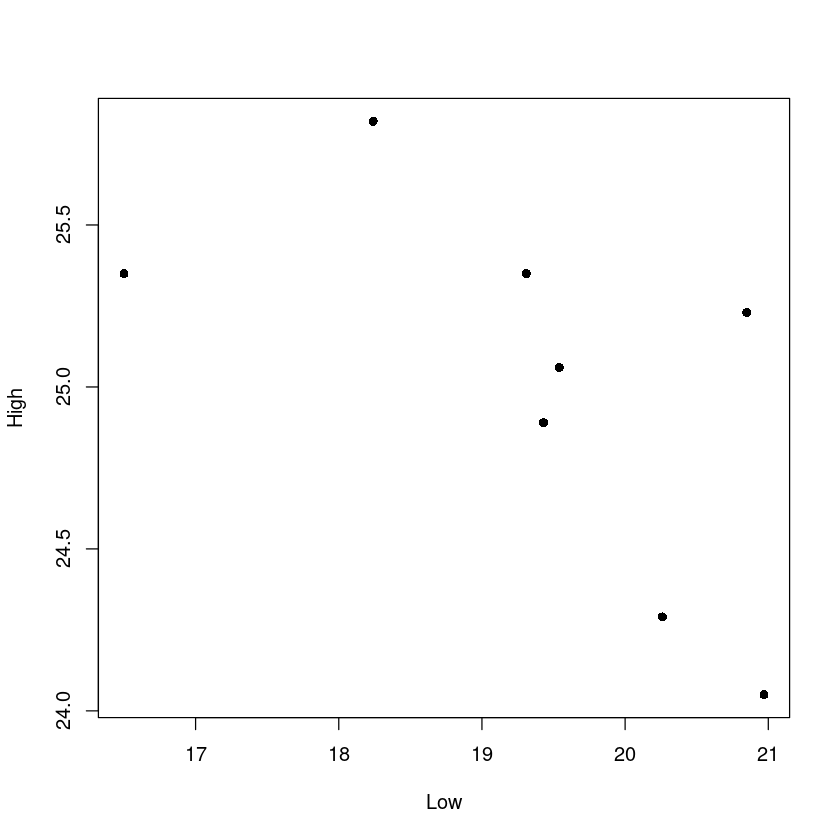
1960년대 아마존강의 최저수위와 최고수위와의 회귀선
df_6_1960 <- df_6[df_6$Year<1970,]df_6_1960$Low_barLow = df_6_1960$Low - mean(df_6_1960$Low)
df_6_1960$High_barHigh = df_6_1960$High - mean(df_6_1960$High) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_6_1960$Low_barLow2 <- df_6_1960$Low_barLow^2
df_6_1960$High_barHigh2 <- df_6_1960$High_barHigh^2
df_6_1960$LowHigh <-df_6_1960$Low_barLow * df_6_1960$High_barHigh- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
round(colSums(df_6_1960),3)- Year
- 15724
- High
- 200.04
- Low
- 155.1
- Low_barLow
- 0
- High_barHigh
- 0
- Low_barLow2
- 15.09
- High_barHigh2
- 2.392
- LowHigh
- -3.761
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
df_6_1960| Year | High | Low | Low_barLow | High_barHigh | Low_barLow2 | High_barHigh2 | LowHigh | |
|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 1962 | 25.82 | 18.24 | -1.1475 | 0.815 | 1.31675625 | 0.664225 | -0.9352125 |
| 2 | 1963 | 25.35 | 16.50 | -2.8875 | 0.345 | 8.33765625 | 0.119025 | -0.9961875 |
| 3 | 1964 | 24.29 | 20.26 | 0.8725 | -0.715 | 0.76125625 | 0.511225 | -0.6238375 |
| 4 | 1965 | 24.05 | 20.97 | 1.5825 | -0.955 | 2.50430625 | 0.912025 | -1.5112875 |
| 5 | 1966 | 24.89 | 19.43 | 0.0425 | -0.115 | 0.00180625 | 0.013225 | -0.0048875 |
| 6 | 1967 | 25.35 | 19.31 | -0.0775 | 0.345 | 0.00600625 | 0.119025 | -0.0267375 |
| 7 | 1968 | 25.23 | 20.85 | 1.4625 | 0.225 | 2.13890625 | 0.050625 | 0.3290625 |
| 8 | 1969 | 25.06 | 19.54 | 0.1525 | 0.055 | 0.02325625 | 0.003025 | 0.0083875 |
beta1_1960 <- as.numeric(colSums(df_6_1960)[8]/colSums(df_6_1960)[6])
beta0_1960 <- mean(df_6_1960$High) - beta1_1960 * mean(df_6_1960$Low)cat("hat beta0 1960 = ", round(beta0_1960,4))
cat("\nhat beta1 1960 = ", round(beta1_1960,4))hat beta0 1960 = 29.8367
hat beta1 1960 = -0.2492cat("회귀선은 다음과 같았다. 1960 High = ",round(beta0_1960,4)," + ", round(beta1_1960,4),"Low")회귀선은 다음과 같았다. 1960 High = 29.8367 + -0.2492 LowR결과 비교
summary(lm(df_6_1960$High~df_6_1960$Low))
Call:
lm(formula = df_6_1960$High ~ df_6_1960$Low)
Residuals:
Min 1Q Median 3Q Max
-0.5606 -0.4053 -0.0057 0.3765 0.5895
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.8367 2.4640 12.109 1.93e-05 ***
df_6_1960$Low -0.2492 0.1268 -1.966 0.0969 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4925 on 6 degrees of freedom
Multiple R-squared: 0.3918, Adjusted R-squared: 0.2904
F-statistic: 3.864 on 1 and 6 DF, p-value: 0.09691SST_1960 = sum((df_6_1960$High - mean(df_6_1960$High))^2)SSR_1960 = sum( ( (29.8367 + -0.2492*df_6_1960$Low)-mean(df_6_1960$High) )^2 )SSE_1960 = sum( ( df_6_1960$High-(29.8367 + -0.2492*df_6_1960$Low))^2 )cat("1960 SST = ", SST_1960,", df = 7")
cat("\n1960 SSR = ", SSR_1960,", df = 1")
cat("\n1960 SSE = ", SSE_1960, ", df = 6")1960 SST = 2.3924 , df = 7
1960 SSR = 0.9370965 , df = 1
1960 SSE = 1.455164 , df = 6R결과 비교
anova(lm(df_6_1960$High~df_6_1960$Low))| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | |
| df_6_1960$Low | 1 | 0.9372373 | 0.9372373 | 3.864464 | 0.09690958 |
| Residuals | 6 | 1.4551627 | 0.2425271 | NA | NA |
1970년대 아마존강의 최저수위와 최고수위와의 산점도
plot(df_6$High[df_6$Year>=1970]~df_6$Low[df_6$Year>=1970],
xlab = "Low",
ylab ="High",
pch = 16,
cex = 1)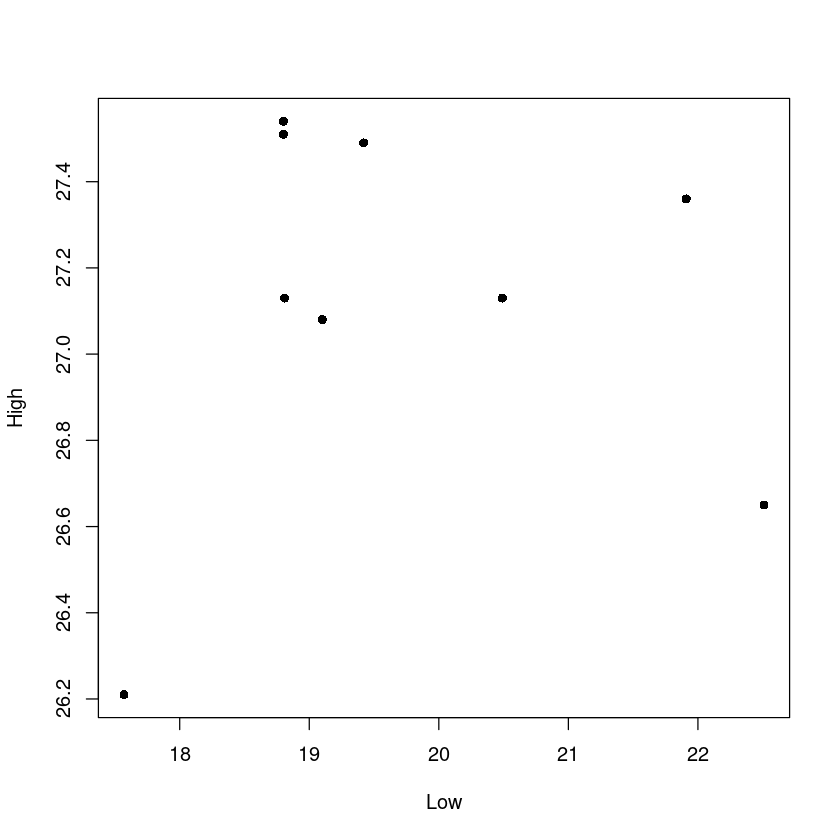
1970년대 아마존강의 최저수위와 최고수위와의 회귀선
df_6_1970 <- df_6[df_6$Year>=1970,]df_6_1970$Low_barLow = df_6_1970$Low - mean(df_6_1970$Low)
df_6_1970$High_barHigh = df_6_1970$High - mean(df_6_1970$High) - \(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.
df_6_1970$Low_barLow2 <- df_6_1970$Low_barLow^2
df_6_1970$High_barHigh2 <- df_6_1970$High_barHigh^2
df_6_1970$LowHigh <-df_6_1970$Low_barLow * df_6_1970$High_barHigh- \(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.
round(colSums(df_6_1970),3)- Year
- 17766
- High
- 244.1
- Low
- 177.41
- Low_barLow
- 0
- High_barHigh
- 0
- Low_barLow2
- 20.79
- High_barHigh2
- 1.574
- LowHigh
- 0.338
\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)
\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)
df_6_1970| Year | High | Low | Low_barLow | High_barHigh | Low_barLow2 | High_barHigh2 | LowHigh | |
|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 9 | 1970 | 27.13 | 20.49 | 0.7777778 | 0.007777778 | 0.60493827 | 6.049383e-05 | 0.006049383 |
| 10 | 1971 | 27.36 | 21.91 | 2.1977778 | 0.237777778 | 4.83022716 | 5.653827e-02 | 0.522582716 |
| 11 | 1972 | 26.65 | 22.51 | 2.7977778 | -0.472222222 | 7.82756049 | 2.229938e-01 | -1.321172840 |
| 12 | 1973 | 27.13 | 18.81 | -0.9022222 | 0.007777778 | 0.81400494 | 6.049383e-05 | -0.007017284 |
| 13 | 1974 | 27.49 | 19.42 | -0.2922222 | 0.367777778 | 0.08539383 | 1.352605e-01 | -0.107472840 |
| 14 | 1975 | 27.08 | 19.10 | -0.6122222 | -0.042222222 | 0.37481605 | 1.782716e-03 | 0.025849383 |
| 15 | 1976 | 27.51 | 18.80 | -0.9122222 | 0.387777778 | 0.83214938 | 1.503716e-01 | -0.353739506 |
| 16 | 1977 | 27.54 | 18.80 | -0.9122222 | 0.417777778 | 0.83214938 | 1.745383e-01 | -0.381106173 |
| 17 | 1978 | 26.21 | 17.57 | -2.1422222 | -0.912222222 | 4.58911605 | 8.321494e-01 | 1.954182716 |
beta1_1970 <- as.numeric(colSums(df_6_1970)[8]/colSums(df_6_1970)[6])
beta0_1970 <- mean(df_6_1970$High) - beta1_1970 * mean(df_6_1970$Low)cat("hat beta0 1970 = ", round(beta0_1970,4))
cat("\nhat beta1 1970 = ", round(beta1_1970,4))hat beta0 1970 = 26.8016
hat beta1 1970 = 0.0163R결과 비교
summary(lm(df_6_1970$High~df_6_1970$Low))
Call:
lm(formula = df_6_1970$High ~ df_6_1970$Low)
Residuals:
Min 1Q Median 3Q Max
-0.87738 -0.03226 0.02245 0.37253 0.43262
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.80160 2.05235 13.059 3.6e-06 ***
df_6_1970$Low 0.01627 0.10381 0.157 0.88
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4733 on 7 degrees of freedom
Multiple R-squared: 0.003495, Adjusted R-squared: -0.1389
F-statistic: 0.02455 on 1 and 7 DF, p-value: 0.8799cat("회귀선은 다음과 같았다. 1970 High = ",round(beta0_1970,4)," + ", round(beta1_1970,4),"Low")회귀선은 다음과 같았다. 1970 High = 26.8016 + 0.0163 LowSST_1970 = sum((df_6_1970$High - mean(df_6_1970$High))^2)SSR_1970 = sum( ( (26.8016 + 0.0163 *df_6_1970$Low)-mean(df_6_1970$High) )^2 )SSE_1970 = sum( ( df_6_1970$High-(26.8016 + 0.0163 *df_6_1970$Low))^2 )cat("1970 SST = ", SST_1970,", df = 8")
cat("\n1970 SSR = ", SSR_1970,", df = 1")
cat("\n1970 SSE = ", SSE_1970, ", df = 7")1970 SST = 1.573756 , df = 8
1970 SSR = 0.005528037 , df = 1
1970 SSE = 1.56826 , df = 7R결과 비교
anova(lm(df_6_1970$High~df_6_1970$Low))| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | |
| df_6_1970$Low | 1 | 0.005500107 | 0.005500107 | 0.02455005 | 0.8799168 |
| Residuals | 7 | 1.568255449 | 0.224036493 | NA | NA |
(5)
아마존강의 최저수위와 최고수위와의 관계가 1960년대와 1970년대에 따라 차이가 있는가? 두 회귀모형의 동일성 여부를 유의수준 \(\alpha = 0.01\)에서 검정하시오.
Answer
가설
\(H_0 : \beta_{01} = \beta_{02} \text{ and } \beta_{11} = \beta_{12}\)
\(H_1 : \beta_{01} \neq \beta_{02} \text{ pr } \beta_{11} \neq \beta_{12}\)
(2)에서 구했던 것
\(\text{High} = 26.40088 -0.01406\text{Low}\)
SST = sum((df_6$High - mean(df_6$High))^2)SSR = sum( ( (26.40088 - 0.01406 *df_6$Low)-mean(df_6$High) )^2 )SSE = sum( ( df_6$High-(26.40088 - 0.01406 *df_6$Low))^2 )cat("SST = ", SST,", df = 16")
cat("\nSSR = ", SSR,", df = 1")
cat("\nSSE = ", SSE, ", df = 15")SST = 22.95141 , df = 16
SSR = 0.007181232 , df = 1
SSE = 22.94423 , df = 15R결과와 비교
anova(lm(df_6$High~df_6$Low))| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | |
| df_6$Low | 1 | 0.007180811 | 0.007180811 | 0.00469452 | 0.9462794 |
| Residuals | 15 | 22.944230954 | 1.529615397 | NA | NA |
\(\text{1960 High} = 29.8367 + -0.2492\text{Low}\)
cat("1960 SST = ", SST_1960,", df = 7")
cat("\n1960 SSR = ", SSR_1960,", df = 1")
cat("\n1960 SSE = ", SSE_1960, ", df = 6")1960 SST = 2.3924 , df = 7
1960 SSR = 0.9370965 , df = 1
1960 SSE = 1.455164 , df = 6\(\text{1970 High} = 26.8016 + 0.0163\text{Low}\)
cat("1970 SST = ", SST_1970,", df = 8")
cat("\n1970 SSR = ", SSR_1970,", df = 1")
cat("\n1970 SSE = ", SSE_1970, ", df = 7")1970 SST = 1.573756 , df = 8
1970 SSR = 0.005528037 , df = 1
1970 SSE = 1.56826 , df = 7검정통계량
\(F_0 = \frac{SSE(R) - SSE(F)}{df_R} - \times \frac{df_F}{SSE(F)}\)
SSE_F = SSE_1960 + SSE_1970
df_F = 6 + 7SSE_R = SSE
df_R = 15F_0 = (SSE_R - SSE_F)/(df_R - df_F) / (SSE_F/df_F)
F_0
42.8273639841797
df_R - df_F
2
df_F
13
F_stan = qf(0.95,2,13)cat(F_0, " 는 유의수준 0.05에서 F값 ", F_stan , " 보다 크다.")
cat("\n따라서 귀무가설을 기각하였고, 두 회귀모형은 beta0가 다르거나")
cat("\n혹은 beta1이 다르거나 혹은 beta0,beta1 모두가 다르다.")42.82736 는 유의수준 0.05에서 F값 3.805565 보다 크다.
따라서 귀무가설을 기각하였고, 두 회귀모형은 beta0가 다르거나
혹은 beta1이 다르거나 혹은 beta0,beta1 모두가 다르다.(6)
(4)에서 구한 두 회귀모형의 기울기가 같은지 유의수준 \(\alpha = 0.01\)에서 검정하시오.
Answer
기울기 비교에 대한 가설
\(H_0 : \beta_{11} = \beta_{12} \text{ vs. } H_1 : \beta_{11} \neq \beta_{12}\)
검정통계량
\(t_0 = \frac{ \hat{\beta}_{11} - \hat{\beta}_{12} }{ \sqrt{ \hat{Var}( \hat{\beta}_{11} - \hat{\beta}_{12} ) } }\)
\(\text{Degree of Freedom} = t((n_1 - 1) + (n_2 - 1))\)
\(\hat{Var}( \hat{\beta}_{11} - \hat{\beta}_{12} ) = MSE(F) [\frac{1}{\sum(x_{1j} - \bar{x}_1)^2} + \frac{1}{\sum(x_{2j} - \bar{x}_2)^2}]\)
round(beta1_1960,4)
-0.2492
round(beta1_1970,4)
0.0163
SSE_F
3.02342329210101
MSE_F = SSE_F / df_F
MSE_F
0.232571022469308
sum(df_6_1960$Low_barLow2)
15.08995
sum(df_6_1970$Low_barLow2)
20.7903555555556
var_diff = MSE_F * (1/sum(df_6_1960$Low_barLow2) + 1/sum(df_6_1970$Low_barLow2))
var_diff
0.026598798385161
t_0 = (beta1_1960 - beta1_1970)/sqrt(var_diff)
t_0
-1.62782282241728
qt(0.995,df_F)
3.01227583871658
cat(t_0,"는 ",qt(0.995,df_F),"보다 작다.")
cat("\n따라서 유의수준 1%에서 귀무가설을 기각하지 못하여 두 회귀모형의 기울기가 같다고 할 수 있다.")-1.627823 는 3.012276 보다 작다.
따라서 유의수준 1%에서 귀무가설을 기각하지 못하여 두 회귀모형의 기울기가 같다고 할 수 있다.\(H_0 : \beta_{11} = \beta_{12}\) 채택