Seoyeon’s Blog for classes

기계학습 특강 (6주차) 10월5일 Homework

imports

import torch
import torchvision
from fastai.data.all import *
import matplotlib.pyplot as plt

숙제 (해설 및 풀이는 여기참고)

숫자0과 숫자1을 구분하는 네트워크를 아래와 같은 구조로 설계하라

\[\underset{(n,784)}{\bf X} \overset{l_1}{\to} \underset{(n,64)}{\boldsymbol u^{(1)}} \overset{a_1}{\to} \underset{(n,64)}{\boldsymbol v^{(1)}} \overset{l_1}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{a_2}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\]

위에서 \(a_1\)은 relu를, \(a_2\)는 sigmoid를 의미한다.

“y=0”은 숫자0을 의미하도록 하고 “y=1”은 숫자1을 의미하도록 설정하라.

path = untar_data(URLs.MNIST)

zero_fnames = (path/'training/0').ls()

one_fnames = (path/'training/1').ls()

X0 = torch.stack([torchvision.io.read_image(str(zf)) for zf in zero_fnames])

X1 = torch.stack([torchvision.io.read_image(str(of)) for of in one_fnames])

X = torch.concat([X0,X1],axis=0).reshape(-1,1*28*28).float()

y = torch.tensor([0.0]*len(X0) + [1.0]*len(X1)).reshape(-1,1)

torch.manual_seed(12345)
net = torch.nn.Sequential(
    torch.nn.Linear(784,64),
    torch.nn.ReLU(),
    torch.nn.Linear(64,1),
    torch.nn.Sigmoid()
)

아래의 지침에 따라 200 epoch 학습을 진행하라.

손실함수는 BECLoss를 이용할 것. torch.nn.BCELoss() 를 이용할 것.
옵티마이저는 아담으로 설정할 것. 학습률은 lr=0.002로 설정할 것.

loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters(),lr=0.002)

for epoc in range(200):
    yhat = net(X)
    loss = loss_fn(yhat,y)
    loss.backward()
    optimizr.step()
    optimizr.zero_grad()

plt.plot(y)
plt.plot(yhat.data,'.',alpha=0.4)

아래의 지침에 따라 200 epoch 학습을 진행하라. 학습이 잘 되는가?

손실함수는 BECLoss를 이용할 것. torch.nn.BCELoss()를 사용하지 않고 수식을 직접 입력할 것.
옵티마이저는 아담으로 설정할 것. 학습률은 lr=0.002로 설정할 것.

torch.manual_seed(12345)
net = torch.nn.Sequential(
    torch.nn.Linear(784,64),
    torch.nn.ReLU(),
    torch.nn.Linear(64,1),
    torch.nn.Sigmoid()
)

optimizr = torch.optim.Adam(net.parameters(),lr=0.002)

for epoc in range(200):
    yhat = net(X)
    loss = -torch.mean(y*torch.log(yhat) + (1-y)*torch.log(1-yhat))
    loss.backward()
    optimizr.step()
    optimizr.zero_grad()

plt.plot(y)
plt.plot(yhat.data,'.',alpha=0.4)

yhat.data

tensor([[nan],
        [nan],
        [nan],
        ...,
        [nan],
        [nan],
        [nan]])

학습이 잘 되지 않았다.

아래의 지침에 따라 200 epoch 학습을 진행하라. 학습이 잘 되는가?

이미지의 값을 0과 1사이로 규격화 하라. (Xnp = Xnp/255 를 이용하세요!)
손실함수는 BECLoss를 이용할 것. torch.nn.BCELoss()를 사용하지 않고 수식을 직접 입력할 것.
옵티마이저는 아담으로 설정할 것. 학습률은 lr=0.002로 설정할 것.

X = X/255

torch.manual_seed(12345)
net = torch.nn.Sequential(
    torch.nn.Linear(784,64),
    torch.nn.ReLU(),
    torch.nn.Linear(64,1),
    torch.nn.Sigmoid()
)

optimizr=torch.optim.Adam(net.parameters(),lr=0.002)

for epoc in range(200):
    yhat = net(X)
    loss = -torch.mean(y*torch.log(yhat) + (1-y)*torch.log(1-yhat))
    loss.backward()
    optimizr.step()
    optimizr.zero_grad()

plt.plot(y)
plt.plot(yhat.data,'.',alpha=0.4)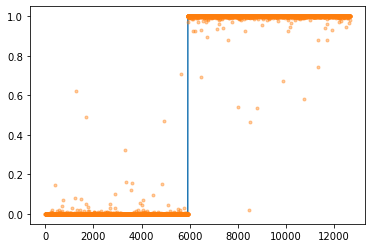

아래와 같은 수식을 이용하여 accuracy를 계산하라.

\(\text{accuracy}=\frac{1}{n}\sum_{i=1}^n I(\tilde{y}_i=y_i)\) - \(\tilde{y}_i = \begin{cases} 1 & \hat{y}_i > 0.5 \\ 0 & \hat{y}_i \leq 0.5 \end{cases}\) - \(I(\tilde{y}_i=y_i) = \begin{cases} 1 & \tilde{y}_i=y_i \\ 0 & \tilde{y}_i \neq y_i \end{cases}\)

단, \(n\)은 0과 1을 의미하는 이미지의 수

ytilde = (yhat > 0.5) * 1

ytilde

tensor([[0],
        [0],
        [0],
        ...,
        [1],
        [1],
        [1]])

(ytilde == y) * 1

tensor([[1],
        [1],
        [1],
        ...,
        [1],
        [1],
        [1]])

torch.sum((ytilde == y) * 1)

tensor(12661)

torch.sum((ytilde == y) * 1)/len(y)

tensor(0.9997)

print("accuraccy: ",torch.sum((ytilde == y) * 1)/len(y))

accuraccy:  tensor(0.9997)