고급회귀분석 CH10

이상치

library(ggplot2)

회귀진단

1. 오차항의 검토
2. 적절한 모형의 선택
3. 독립변수들 간의 상관관계 검토
4. 지렛대점(leverage point)의 검출
5. 이상치(outlier) 화인
6. 영향점(influential observation)의 검출

추정된 회귀직선

\[\hat{y} = X(X^\top X)^{-1} X^\top y = Hy\]

H: hat matrix, \(n \times n\) matrix

\(Var(\hat{y}) = \sigma^2 H\)

\(Var(e) = (I_N - H) \sigma^2\)

\(h_{i,j} = x_i^\top (X^\top X) ^{-1} x_j\)

\(h_{ij}\) : H의 대각원소

\(H = X(X^\top X)^{-1} X^\top\)

\(HH = H\)

\(rank(H) = p+1\)

\(tr(H) = \sum^n_{i=1}h_{ii} = p+1\)

\(H\) : 양반정치행렬 positive definite

\(0 \le h_{ii} <1 , -\frac{1}{2} \le h_{ij} \le -\frac{1}{2}\)

\(p=1, h_{ii} = \frac{1}{n} + \frac{(x_{u} - \bar{x})^2}{S_{xx}}\)

\(p>1, h_{ii} = \frac{1}{n} + (x_i - \bar{x})^\top (X^\top X)^{-1} (x_i - \bar{x})\)

지렛대점(leverage point)

\(h_{ii} > s\bar{h}\) 이면, i번째 관측치가 leverage point로 고려 가능

\[\bar{h} = \frac{1}{n} \sum^n_{i=1}h_{ii} = \frac{p+1}{n}\]

잔차(Residual)

\(e = y − \hat{y} = y − X \hat{\beta}\)

\(= y − X(X^\top X)^{-1} X^\top y\)

\(= (In − X(X^\to X)^{-1}X^\to )y = (I_n − H)y\)

\(E(e) = 0_n, Var(e) = (I_n − H)σ^2\)

\(E(e_i) = 0, Var(e_i) = (1 − h_{ii})σ^2\)

\(Cov(e_i,e_j) = −h_{ij} σ^2\)

\(ρ_{ij} = \frac{−h_{ij} σ^2}{ \sqrt{(1 − h_{ii})(1 − h_{jj})σ^4} }=\frac{ −h_{ij}}{\sqrt{(1 − h_{ii})(1 − h_{jj})}}\)

표준화잔차(standardized residual)

\(y \sim N(Xβ,I_nσ^2)\)

\(e \sim N(0_n,(I_n−H)σ^2)\)

\(e_i \sim N(0,(1−h_{ii})σ^2)\)

\(\star \frac{e_i}{\sigma\sqrt{1-h_{ii}}} \sim N(0,1)\)

내적 스튜던트화 잔차(internally studentized residual)

\(r_i = \frac{e_i}{\hat{\sigma}\sqrt{1−h_{ii}}}\)

\(\hat{\sigma}^2 = MSE\)

이러한 표준화 잔차에 대한 표본분포는 분자와 분모가 서로 독립이 아니기 때문에 \(t\) 분포로 근사할 수 없는데, \(|e_i|\)가 큰 경우, \(s\)도 역시 커지게 되기 때문이다.

외적 스튜던트화 잔차(externally studentized residual)

\(r_i^{*} = \frac{e_i}{\hat{\sigma}_{(i)}\sqrt{1 − h_{ii}}} \sim t(n-p-1-1)\)

\(\hat{\sigma}^2_{(i)} = [(n-p-1)\hat{\sigma} - \frac{e^2_{(i)}}{1-h_{ii}}]/(n-p-2)\)

\(|r_i^{*}| ≥ t_{α/2}(n − p − 2)\) 이면 유의수준\(\alpha\)에서 \(y_i\)를 이상점이라고 판정

\(\star\)

\(t_{i} = \frac{y_i - \tilde{y}_i}{\hat{\sigma}\sqrt{1 + x_i^\top [X{i}^\top X(i)]^{-1} x_i}} \sim t(n-p-2)\)

\(|r_i^{*}| \sim t_{i}\)

예제 10.1

df = data.frame('x' =  c(15, 26, 10, 9, 15, 20, 18, 11, 8, 20, 7, 9, 10, 11, 11, 10, 12, 42, 17, 11, 10),
    'y' = c(95, 71, 83, 91, 102, 87, 93, 100, 104, 94, 113, 96, 83, 84, 102, 100, 105, 57, 121, 86, 100))

model = lm(y~x,df)

summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.604  -8.731   1.396   4.523  30.285 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 109.8738     5.0678  21.681 7.31e-15 ***
x            -1.1270     0.3102  -3.633  0.00177 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 11.02 on 19 degrees of freedom
Multiple R-squared:   0.41, Adjusted R-squared:  0.3789 
F-statistic:  13.2 on 1 and 19 DF,  p-value: 0.001769

\(y = 109.8738 -1.1270 x\)

plot(df$x,df$y)
abline(model, col='steelblue', lwd=2)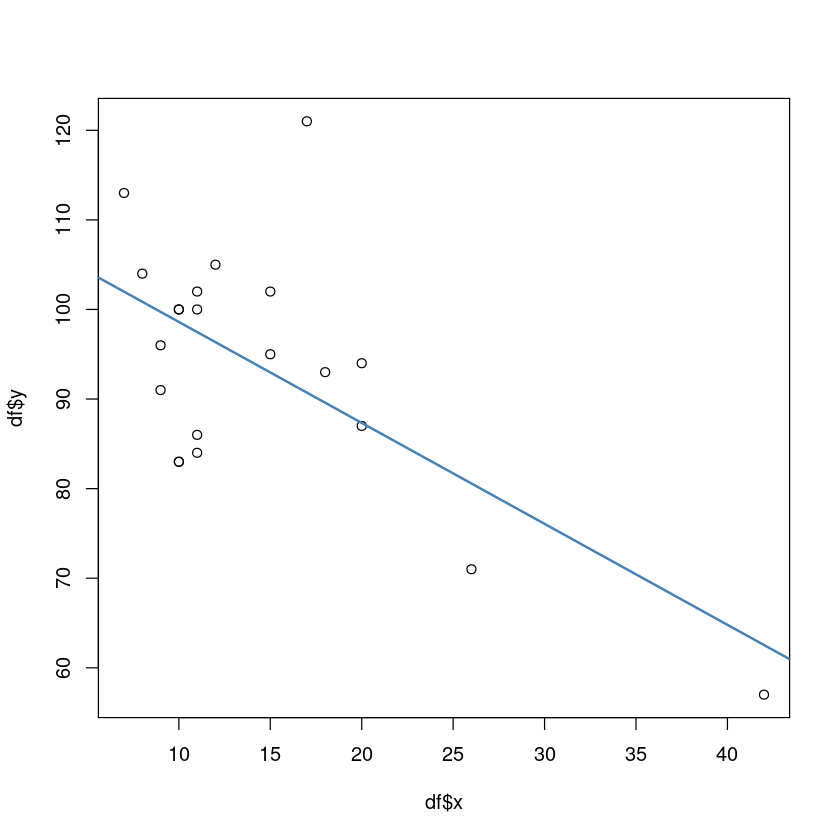

anova(model)

A anova: 2 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x	1	1604.081	1604.0809	13.20182	0.001768622
Residuals	19	2308.586	121.5045	NA	NA

qf(0.95,1,19)

4.3807496923318

\(F_0 = 13.20 > F_{0.05}(1,19) = 4.38\), 회귀직선은 유의하다

\(\sigma^2 \sim MSE\)

MSE = 121.505

sqrt(MSE)

11.0229306447968

손계산

res = df$y - (109.874 - 1.127*df$x)

h = 1/21 + (df$x - mean(df$x))^2/(1604.08)

ri = res/(sqrt(MSE)*sqrt(1-h))

ri2 = res/(((19*sqrt(MSE) - res^2/(1-h))/18)*sqrt(1-h))

rstudent(model)

1

0.183968493379394

2

-0.941583351378201

3

-1.51081192291799

4

-0.814263363159438

5

0.832862917520795

6

-0.030631827537088

7

0.311246764732158

8

0.229715749649931

9

0.289910136925676

10

0.617660260595883

11

1.05084716358865

12

-0.342831483529281

13

-1.51081192291799

14

-1.27977575448039

15

0.413153195694502

16

0.127393415386012

17

0.798281144415116

18

-0.845110861537551

19

3.60697972130439

20

-1.07648107628971

21

0.127393415386012

rstudent(model)[abs(rstudent(model))>qt(0.975,258)]

19: 3.60697972130439

round(data.frame(rep(1:21),res,h,ri,ri2),4)

A data.frame: 21 × 5

rep.1.21.	res	h	ri	ri2
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	2.031	0.0479	0.1888	0.1827
2	-9.572	0.1318	-0.9319	-1.7796
3	-15.604	0.0596	-1.4598	5.8540
4	-8.731	0.0657	-0.8194	-1.2717
5	9.031	0.0479	0.8396	1.3459
6	-0.334	0.0673	-0.0314	-0.0297
7	3.412	0.0558	0.3185	0.3207
8	2.523	0.0547	0.2354	0.2304
9	3.142	0.0730	0.2961	0.2955
10	6.666	0.0673	0.6262	0.7679
11	11.015	0.0816	1.0427	2.6755
12	-3.731	0.0657	-0.3502	-0.3571
13	-15.604	0.0596	-1.4598	5.8540
14	-13.477	0.0547	-1.2575	-14.4335
15	4.523	0.0547	0.4220	0.4459
16	1.396	0.0596	0.1306	0.1250
17	8.650	0.0512	0.8056	1.2241
18	-5.540	0.5232	-0.7278	-0.9954
19	30.285	0.0519	2.8216	-0.7386
20	-11.477	0.0547	-1.0709	-3.0318
21	1.396	0.0596	0.1306	0.1250

\(2\bar{h}\)

2*(2/21)

0.19047619047619

18번째가 2hbar 보다 크니까 지렛대점

qt(0.975,18)

2.10092204024104

19번째가 ri2 t보다 크니까 이상점

summary(influence.measures( model))

Potentially influential observations of
     lm(formula = y ~ x, data = df) :

   dfb.1_ dfb.x   dffit   cov.r   cook.d hat    
18  0.83  -1.11_* -1.16_*  2.96_*  0.68   0.65_*
19  0.14   0.27    0.85    0.40_*  0.22   0.05  

영향점(influential observation)

DIFFITS

\(DIFFITS(i) = (\frac{h_{ii}}{10h_{ii}})^{1/2} r^{*}_i\)

\(DIFFITS(i) \ge 2(\frac{p+1}{n})^{1/2}\) 이 되는 i번째 관측칠가 영향점이라고 말함

Cook의 통계량

\(D(i) = \frac{r^2_i}{p+1} \frac{h_{ii}}{1-h_{ii}}\)

대략적으로 \(D(i) \ge F_{0.5}(p+1,n-p-1)\)이면 영향을 크게 주는 측정값으로 의심

h

hatvalues(model)

1

0.0479224794510218

2

0.154513234296056

3

0.0628157755825353

4

0.0705452077520549

5

0.0479224794510218

6

0.0726189578463163

7

0.0579895935449815

8

0.0566699343940879

9

0.0798582309026469

10

0.0726189578463163

11

0.0907548450343111

12

0.0705452077520549

13

0.0628157755825353

14

0.0566699343940879

15

0.0566699343940879

16

0.0628157755825353

17

0.0521076841867129

18

0.65160998416409

19

0.0530502978659226

20

0.0566699343940879

21

0.0628157755825353

diffits

dffits(model)

1

0.0412740357514056

2

-0.402520687302525

3

-0.391140045474215

4

-0.224328533660804

5

0.186855983882421

6

-0.00857173640678122

7

0.0772239528389379

8

0.0563034865220476

9

0.085407472693718

10

0.172840518129759

11

0.331996853994253

12

-0.0944496430423618

13

-0.391140045474215

14

-0.313673908094842

15

0.101264129345836

16

0.0329813827461469

17

0.187166128054405

18

-1.15577873097521

19

0.853737107130766

20

-0.263846244162542

21

0.0329813827461469

cooksdistance, D

cooks.distance(model)

1

0.000897406392870691

2

0.0814979551507635

3

0.0716581442213833

4

0.0256159582452641

5

0.0177436626335013

6

3.87762740910137e-05

7

0.0031305748029949

8

0.00166820857813469

9

0.00383194880672965

10

0.0154395158127621

11

0.0548101351203612

12

0.00467762256482442

13

0.0716581442213833

14

0.0475978118328145

15

0.00536121617564154

16

0.000573584529113046

17

0.017856495213809

18

0.678112028575845

19

0.223288273631179

20

0.0345188940892692

21

0.000573584529113046

COVRATIO

covratio(model) 

1

1.16589181683219

2

1.19699897676296

3

0.936347397341839

4

1.11510268993929

5

1.08504108257728

6

1.20131998275497

7

1.17015757898673

8

1.17423726760803

9

1.19966823450598

10

1.15209128858604

11

1.08783960928084

12

1.18326164825873

13

0.936347397341839

14

0.992331347870996

15

1.15904532932769

16

1.18673688685713

17

1.09643883044992

18

2.95868271380702

19

0.396431612340971

20

1.04257281407241

21

1.18673688685713

influence.measures( model)

Influence measures of
     lm(formula = y ~ x, data = df) :

     dfb.1_    dfb.x    dffit cov.r   cook.d    hat inf
1   0.01664  0.00328  0.04127 1.166 8.97e-04 0.0479    
2   0.18862 -0.33480 -0.40252 1.197 8.15e-02 0.1545    
3  -0.33098  0.19239 -0.39114 0.936 7.17e-02 0.0628    
4  -0.20004  0.12788 -0.22433 1.115 2.56e-02 0.0705    
5   0.07532  0.01487  0.18686 1.085 1.77e-02 0.0479    
6   0.00113 -0.00503 -0.00857 1.201 3.88e-05 0.0726    
7   0.00447  0.03266  0.07722 1.170 3.13e-03 0.0580    
8   0.04430 -0.02250  0.05630 1.174 1.67e-03 0.0567    
9   0.07907 -0.05427  0.08541 1.200 3.83e-03 0.0799    
10 -0.02283  0.10141  0.17284 1.152 1.54e-02 0.0726    
11  0.31560 -0.22889  0.33200 1.088 5.48e-02 0.0908    
12 -0.08422  0.05384 -0.09445 1.183 4.68e-03 0.0705    
13 -0.33098  0.19239 -0.39114 0.936 7.17e-02 0.0628    
14 -0.24681  0.12536 -0.31367 0.992 4.76e-02 0.0567    
15  0.07968 -0.04047  0.10126 1.159 5.36e-03 0.0567    
16  0.02791 -0.01622  0.03298 1.187 5.74e-04 0.0628    
17  0.13328 -0.05493  0.18717 1.096 1.79e-02 0.0521    
18  0.83112 -1.11275 -1.15578 2.959 6.78e-01 0.6516   *
19  0.14348  0.27317  0.85374 0.396 2.23e-01 0.0531   *
20 -0.20761  0.10544 -0.26385 1.043 3.45e-02 0.0567    
21  0.02791 -0.01622  0.03298 1.187 5.74e-04 0.0628