Definition

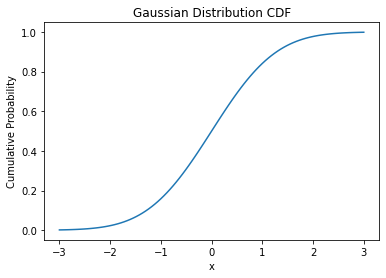
CDF(Cumulative Distribution Function) 누적 분포 함수

가우시안 분포

\[F(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^x e^{\frac{1}{2} (\frac{x-\mu}{\sigma})^2}, -\infty < x< \infty\]

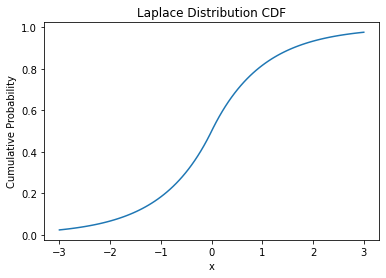
라플라스 분포Laplace distribution

\[F(x) = \begin{cases} \frac{1}{2}e^{\frac{x-\mu}{b}} & if x \le \mu \\ 1-\frac{1}{2}e^{-\frac{x-\mu}{b}} & if x \ge \mu \end{cases}\]

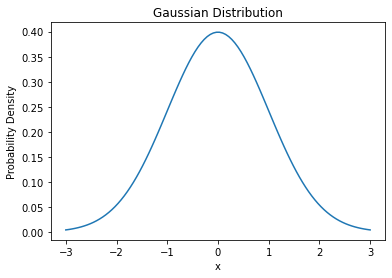
PDF(Probability Distribution Function) 확률 밀도 함수

가우시안 분포

\[f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{\frac{1}{2} (\frac{x-\mu}{\sigma})^2}, -\infty < x< \infty\]

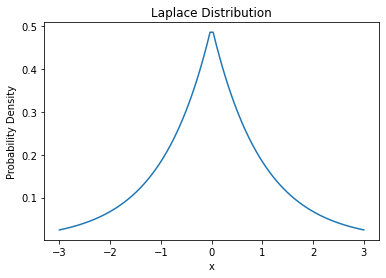
라플라스 분포Laplace distribution

\[f(x) = \frac{1}{2b}e^{-\frac{|x-\mu|}{b}}, -\infty < x< \infty\]

CDF

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, laplace

# 가우시안 분포
mu = 0  # 평균
sigma = 1  # 표준편차

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # x 값 범위 설정
gaussian_cdf = norm.cdf(x, loc=mu, scale=sigma)  # 가우시안 분포 CDF

plt.plot(x, gaussian_cdf)
plt.title('Gaussian Distribution CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.show()

# 라플라스 분포
loc = 0  # 평균
scale = 1  # 스케일 매개변수

laplace_cdf = laplace.cdf(x, loc=loc, scale=scale)  # 라플라스 분포 CDF

plt.plot(x, laplace_cdf)
plt.title('Laplace Distribution CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.show()

PDF

import numpy as np
import matplotlib.pyplot as plt

# 가우시안 분포
mu = 0  # 평균
sigma = 1  # 표준편차

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # x 값 범위 설정
gaussian = np.exp(-(x - mu)**2 / (2 * sigma**2)) / (sigma * np.sqrt(2 * np.pi))  # 가우시안 분포 함수

plt.plot(x, gaussian)
plt.title('Gaussian Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

# 라플라스 분포
loc = 0  # 평균
scale = 1  # 스케일 매개변수

laplace = np.exp(-np.abs(x - loc) / scale) / (2 * scale)  # 라플라스 분포 함수

plt.plot(x, laplace)
plt.title('Laplace Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

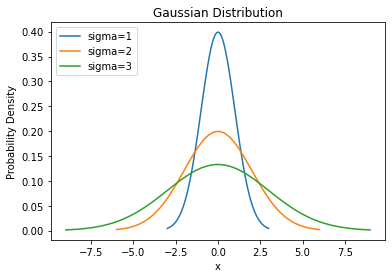
sigma/scale이 다를때

# 가우시안 분포
mu = 0  # 평균
sigma = 1  # 표준편차

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # x 값 범위 설정
gaussian = np.exp(-(x - mu)**2 / (2 * sigma**2)) / (sigma * np.sqrt(2 * np.pi))  # 가우시안 분포 함수

plt.plot(x, gaussian,label='sigma=1')
plt.title('Gaussian Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')

sigma = 2  # 표준편차

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # x 값 범위 설정
gaussian = np.exp(-(x - mu)**2 / (2 * sigma**2)) / (sigma * np.sqrt(2 * np.pi))  # 가우시안 분포 함수

plt.plot(x, gaussian,label='sigma=2')

sigma = 3  # 표준편차

x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # x 값 범위 설정
gaussian = np.exp(-(x - mu)**2 / (2 * sigma**2)) / (sigma * np.sqrt(2 * np.pi))  # 가우시안 분포 함수

plt.plot(x, gaussian,label='sigma=3')
plt.legend(loc='upper left',facecolor='white', frameon=True)

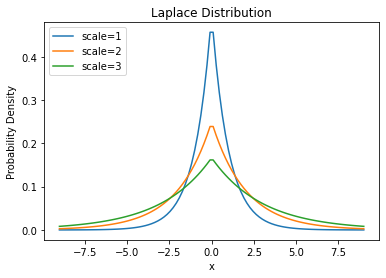
# 라플라스 분포
loc = 0  # 평균
scale = 1  # 스케일 매개변수

laplace = np.exp(-np.abs(x - loc) / scale) / (2 * scale)  # 라플라스 분포 함수

plt.plot(x, laplace,label='scale=1')
plt.title('Laplace Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')

scale = 2  # 스케일 매개변수

laplace = np.exp(-np.abs(x - loc) / scale) / (2 * scale)  # 라플라스 분포 함수

plt.plot(x, laplace,label='scale=2')

scale = 3  # 스케일 매개변수

laplace = np.exp(-np.abs(x - loc) / scale) / (2 * scale)  # 라플라스 분포 함수

plt.plot(x, laplace,label='scale=3')
plt.legend(loc='upper left',facecolor='white', frameon=True)