Tree

Tree

전위 순회(preorder traversal)

노드를 방문한다.
왼쪽 서브 트리를 전위 순회한다.
오른쪽 서브 트리를 전위 순회한다.

(쉽게 생각하면 중간->왼쪽->오른쪽 순)

def pre_order(data, left_node, right_node):
    print(data,end='')
    if left_node != '.' :
        pre_order(tree[left_node])
    if right_node != '.' :
        pre_order(tree[right_node])

pre_order()

중위 순회(inorder traversal)

왼쪽 서브 트리를 중위 순회한다.
노드를 방문한다.
오른쪽 서브 트리를 중위 순회한다.

(쉽게 생각하면 왼쪽->중간->오른쪽 순)

def in_order(data, left_node, right_node):
    if left_node != '.' :
        pre_order(tree[left_node])
    print(data,end='')
    if right_node != '.' :
        pre_order(tree[right_node])

휘위 순회(postorder traversal)

왼쪽 서브 트리를 후위 순회한다.
오른쪽 서브 트리를 후위 순회한다.
노드를 방문한다.

(쉽게 생각하면 왼쪽->오른쪽->중간 순)

def post_order(data, left_node, right_node):
    if left_node != '.' :
        pre_order(tree[left_node])
    if right_node != '.' :
        pre_order(tree[right_node])
    print(data,end='')

이진 검색 트리

이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.

노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.

노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.

왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.

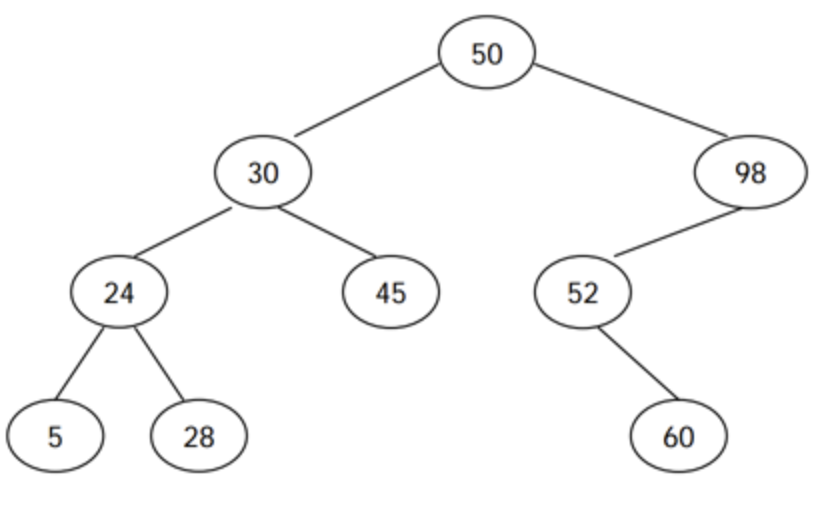
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.

이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.

global something

위 global 에 대한 교수님 수업 자료임!!

\(\star\)

(원칙1) global 에서 정의된 이름은 local 에서 정의된 이름이 없을 경우 그를 대신할 수 있다 (local은 경우에 따라서 global에 있는 변수를 빌려 쓸 수 있다)

(원칙2) local과 global에서 같은 이름 ’x’가 각각 정의되어 있는 경우? global의 변수와 local의 변수는 각각 따로 행동하며 서로 영향을 주지 않는다. (독립적이다)

만약에 local이 global의 변수를 같이 쓰고 있었다고 할지라도, 추후 새롭게 local에 새롭게 같은 이름의 변수가 정의된다면 그 순간 local과 global의 변수를 각자 따로 행동하며 서로 영향을 주지 않는다.

user_input = input("dd: ")
print("dd{}dd".format(user_input))

dd:  d

ddddd

class Node:
    def __init__(self,data):
        self.data = data
        self.left = None
        self.right = None

class Tree:
    def __init__(self):
        self.root = None
        
    def add(self,data):
        if(self.root == None):
            self.root = Node(data)
            
        else:
            current = self.root
            while(True):
                if (current.data > data):
                    if(current.left == None):
                        current.left = Node(data)
                        break
                    current = current.left
                
                if (current.data < data):
                    if(current.right == None):
                        current.right = Node(data)
                        break
                    current = current.right
    def postorder(self,node=None):
        global answer
        if node == None:
            node = self.root
        if node.left != None:
            self.postorder(node.left)
        if node.right != None:
            self.postorder(node.right)
        answer.append(node.data)

# import sys
# sys.setrecursionlimit(200000)

# input = sys.stdin.readline()
input = input()

tree = Tree()

while True:
    try:
        tree.add(int(input()))
    except:
        break

answer = []

tree.postorder()
print('\n'.join(map(str,answer)))

예제 입력 값

tree = Tree()

while True:
    try:
        tree.add(int(input()))
    except:
        break