import torch
from fastai.vision.all import *
import matplotlib.pyplot as plt
import torchvision기계학습 특강 (7주차) 10월19일 [딥러닝의 기초 - 드랍아웃, 이미지자료분석]
imports
import graphviz
def gv(s): return graphviz.Source('digraph G{ rankdir="LR"'+s + '; }');깊은신경망– 오버피팅
데이터
- model: \(y_i = (0\times x_i) + \epsilon_i\)
torch.manual_seed(5)
x=torch.linspace(0,1,100).reshape(100,1)
y=torch.randn(100).reshape(100,1)*0.01
plt.plot(x,y)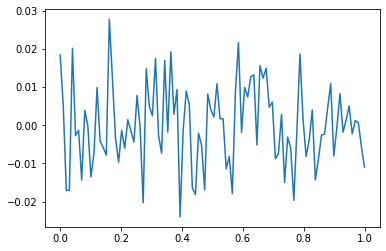
모든 데이터를 사용하여 적합 (512, relu, 1000 epochs)
torch.manual_seed(1)
net = torch.nn.Sequential(
torch.nn.Linear(in_features=1,out_features=512),
torch.nn.ReLU(),
torch.nn.Linear(in_features=512,out_features=1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(1000):
## 1
yhat = net(x)
## 2
loss = loss_fn(yhat,y)
## 3
loss.backward()
## 4
optimizr.step()
optimizr.zero_grad()plt.plot(x,y)
plt.plot(x,net(x).data, '--')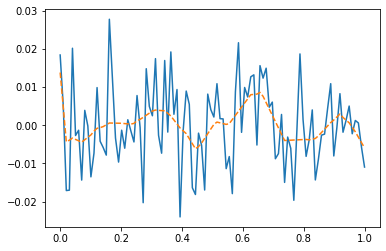
전체데이터를 8:2로 나누어서 8만을 학습
- 데이터를 8:2로 나눈다
xtr = x[:80]
ytr = y[:80]
xtest = x[80:]
ytest = y[80:] x.shape, xtr.shape, xtest.shape(torch.Size([100, 1]), torch.Size([80, 1]), torch.Size([20, 1]))y.shape, ytr.shape, ytest.shape(torch.Size([100, 1]), torch.Size([80, 1]), torch.Size([20, 1]))plt.plot(xtr,ytr,'o')
plt.plot(xtest,ytest,'o')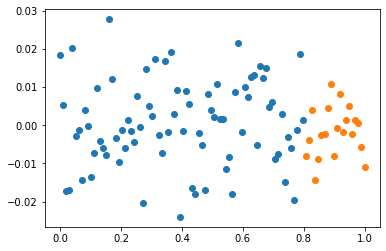
- (xtr,ytr) 만 가지고 net를 학습시킨다.
torch.manual_seed(1)
net = torch.nn.Sequential(
torch.nn.Linear(in_features=1,out_features=512),
torch.nn.ReLU(),
torch.nn.Linear(in_features=512,out_features=1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(1000):
## 1
# yhat
## 2
loss = loss_fn(net(xtr),ytr)
## 3
loss.backward()
## 4
optimizr.step()
optimizr.zero_grad()plt.plot(xtr,ytr,'o')
plt.plot(xtest,ytest,'o')
plt.plot(x,net(x).data,'--k')
#plt.plot(xtr,net(xtr).data,'--k')
#plt.plot(xtest,net(xtest).data,'--k') 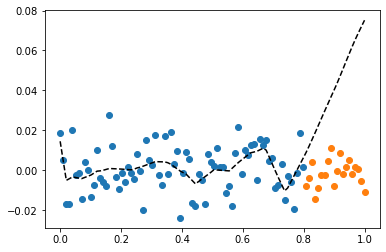
(서연 필기) 오차항이 너무 잘 따라가면 영향을 미칠 수 있다.
데이터에 비해 노드 수가 많으면 오버피팅의 가능성 - 한 변수로 모든 변수 맞추는 우연을 마주한다면? - 모델에 비해 feature가 너무 클때? - 위를 예로 들면 input은 1이었는데 output은 512렸다
차원의 저주
깊은신경망– 드랍아웃
오버피팅의 해결
- 오버피팅의 해결책: 드랍아웃
동등한 초기값에서 시작한다고 설명 - manual_seed 정해준거
torch.manual_seed(1)
net = torch.nn.Sequential(
torch.nn.Linear(in_features=1,out_features=512),
torch.nn.ReLU(),
torch.nn.Dropout(0.8),
torch.nn.Linear(in_features=512,out_features=1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(1000):
## 1
#
## 2
loss = loss_fn(net(xtr),ytr)
## 3
loss.backward()
## 4
optimizr.step()
optimizr.zero_grad()계속 바뀌는 plot
plt.plot(xtr,ytr,'o')
plt.plot(xtest,ytest,'o')
plt.plot(x,net(x).data,'--k')
plt.title(r"network is in training mode",fontsize=15)Text(0.5, 1.0, 'network is in training mode')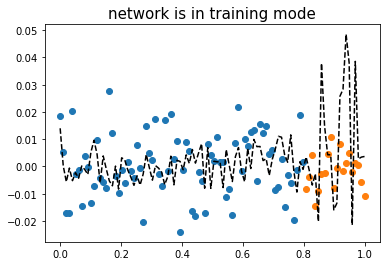
- 올바른 사용법
net.trainingTrueevaliation method 사용
net.eval()
net.trainingFalseplt.plot(xtr,ytr,'o')
plt.plot(xtest,ytest,'o')
plt.plot(x,net(x).data,'--k')
plt.title(r"network is in evaluation mode",fontsize=15)Text(0.5, 1.0, 'network is in evaluation mode')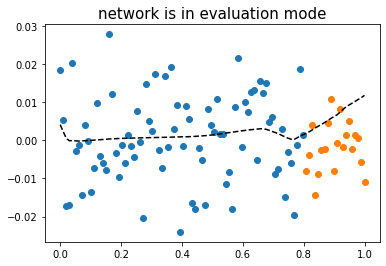
드랍아웃 레이어
_x = torch.linspace(0,1,101)
_x tensor([0.0000, 0.0100, 0.0200, 0.0300, 0.0400, 0.0500, 0.0600, 0.0700, 0.0800,
0.0900, 0.1000, 0.1100, 0.1200, 0.1300, 0.1400, 0.1500, 0.1600, 0.1700,
0.1800, 0.1900, 0.2000, 0.2100, 0.2200, 0.2300, 0.2400, 0.2500, 0.2600,
0.2700, 0.2800, 0.2900, 0.3000, 0.3100, 0.3200, 0.3300, 0.3400, 0.3500,
0.3600, 0.3700, 0.3800, 0.3900, 0.4000, 0.4100, 0.4200, 0.4300, 0.4400,
0.4500, 0.4600, 0.4700, 0.4800, 0.4900, 0.5000, 0.5100, 0.5200, 0.5300,
0.5400, 0.5500, 0.5600, 0.5700, 0.5800, 0.5900, 0.6000, 0.6100, 0.6200,
0.6300, 0.6400, 0.6500, 0.6600, 0.6700, 0.6800, 0.6900, 0.7000, 0.7100,
0.7200, 0.7300, 0.7400, 0.7500, 0.7600, 0.7700, 0.7800, 0.7900, 0.8000,
0.8100, 0.8200, 0.8300, 0.8400, 0.8500, 0.8600, 0.8700, 0.8800, 0.8900,
0.9000, 0.9100, 0.9200, 0.9300, 0.9400, 0.9500, 0.9600, 0.9700, 0.9800,
0.9900, 1.0000])dout = torch.nn.Dropout(0.9)
dout(_x)tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 1.3000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 2.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 2.9000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 4.1000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 5.9000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 7.1000,
0.0000, 0.0000, 0.0000, 0.0000, 7.6000, 7.7000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 8.9000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000])- 90%의 드랍아웃: 드랍아웃층의 입력 중 임의로 90%를 골라서 결과를 0으로 만든다. + 그리고 0이 되지않고 살아남은 값들은 10배 만큼 값이 커진다.
- 드랍아웃레이어 정리 - 구조: 입력 -> 드랍아웃레이어 -> 출력 - 역할: (1) 입력의 일부를 임의로 0으로 만드는 역할 (2) 0이 안된것들은 스칼라배하여 드랍아웃을 통과한 모든 숫자들의 총합이 일정하게 되도록 조정 - 효과: 오버피팅을 억제하는 효과가 있음 (왜??) - 추측일뿐! - 의미: each iteration (each epoch x) 마다 학습에 참여하는 노드가 로테이션으로 랜덤으로 결정됨. - 느낌: 모든 노드가 골고루 학습가능 + 한 두개의 특화된 능력치가 개발되기 보다 평균적인 능력치가 전반적으로 개선됨
(서연 필기) 지배적인 예측 값들보다 비지배적인 예측값을 건들려고 하면 의미가 없음.
이미지자료분석– data
- download data
path = untar_data(URLs.MNIST)- training set
X0 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'training/0').ls()])
X1 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'training/1').ls()])
X = torch.concat([X0,X1])/255
y = torch.tensor([0.0]*len(X0) + [1.0]*len(X1)).reshape(-1,1)- test set
X0 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'testing/0').ls()])
X1 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'testing/1').ls()])
XX = torch.concat([X0,X1])/255
yy = torch.tensor([0.0]*len(X0) + [1.0]*len(X1)).reshape(-1,1)X.shape,XX.shape,y.shape,yy.shape(torch.Size([12665, 1, 28, 28]),
torch.Size([2115, 1, 28, 28]),
torch.Size([12665, 1]),
torch.Size([2115, 1]))이미지자료분석– CNN 예비학습
기존의 MLP 모형
- 교재의 모형
#collapse
gv('''
splines=line
subgraph cluster_1{
style=filled;
color=lightgrey;
"x1"
"x2"
".."
"x784"
label = "Layer 0"
}
subgraph cluster_2{
style=filled;
color=lightgrey;
"x1" -> "node1"
"x2" -> "node1"
".." -> "node1"
"x784" -> "node1"
"x1" -> "node2"
"x2" -> "node2"
".." -> "node2"
"x784" -> "node2"
"x1" -> "..."
"x2" -> "..."
".." -> "..."
"x784" -> "..."
"x1" -> "node30"
"x2" -> "node30"
".." -> "node30"
"x784" -> "node30"
label = "Layer 1: ReLU"
}
subgraph cluster_3{
style=filled;
color=lightgrey;
"node1" -> "y"
"node2" -> "y"
"..." -> "y"
"node30" -> "y"
label = "Layer 2: Sigmoid"
}
''')- 왜 28 by 28 이미지를 784개의 벡터로 만든 다음에 모형을 돌려야 하는가?
- 기존에 개발된 모형이 회귀분석 기반으로 되어있어서 결국 회귀분석 틀에 짜 맞추어서 이미지자료를 분석하는 느낌
- observation의 차원은 \(784\)가 아니라 \(1\times (28\times 28)\)이 되어야 맞다.
새로운 아키텍처의 제시
- 예전
\(\underset{(n,784)}{\bf X} \overset{l_1}{\to} \underset{(n,30)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,30)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\)
- \(l_1\): 선형변환, feature를 뻥튀기하는 역할
- \(\sim\) 꺾인 선이 많아진다
- \(relu\): 뻥튀기된 feature에 비선형을 추가하여 표현력 극대화
- \(l_2\): 선형변환, 뻥튀기된 feature를 요약 하는 역할 (=데이터를 요약하는 역할)
- 새로운 아키텍처 - \(conv\): feature를 뻥튀기하는 역할 (2d ver \(l_1\) 느낌) - \(relu\): - \(pooling\): 데이터를 요약하는 역할
CONV 레이어 (선형변환의 2D 버전)
- 우선 연산하는 방법만 살펴보자.
(예시1)
torch.manual_seed(43052)
_conv = torch.nn.Conv2d(1,1,(2,2)) # 입력1, 출력1, (2,2) window size
_conv.weight.data, _conv.bias.data(tensor([[[[-0.1733, -0.4235],
[ 0.1802, 0.4668]]]]),
tensor([0.2037]))_X = torch.arange(4).reshape(1,1,2,2).float()
_Xtensor([[[[0., 1.],
[2., 3.]]]])(-0.1733)*0 + (-0.4235)*1 +\
(0.1802)*2 + (0.4668)*3 + 0.20371.541_conv(_X)tensor([[[[1.5410]]]], grad_fn=<ThnnConv2DBackward0>)torch.__version__'1.10.1'(예시2) 잘하면 평균도 계산하겠다?
_conv.weight.data = torch.tensor([[[[1/4, 1/4],[1/4,1/4]]]])
_conv.bias.data = torch.tensor([0.0])
_conv.weight.data,_conv.bias.data(tensor([[[[0.2500, 0.2500],
[0.2500, 0.2500]]]]),
tensor([0.]))_conv(_X) , (0+1+2+3)/4(tensor([[[[1.5000]]]], grad_fn=<ThnnConv2DBackward0>), 1.5)(예시3) 이동평균?
_X = torch.arange(0,25).float().reshape(1,1,5,5)
_Xtensor([[[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.],
[15., 16., 17., 18., 19.],
[20., 21., 22., 23., 24.]]]])_conv(_X)tensor([[[[ 3., 4., 5., 6.],
[ 8., 9., 10., 11.],
[13., 14., 15., 16.],
[18., 19., 20., 21.]]]], grad_fn=<ThnnConv2DBackward0>)(예시4) window size가 증가한다면? (2d의 이동평균느낌)
_conv = torch.nn.Conv2d(1,1,(3,3)) # 입력1, 출력1, (3,3) window size
_conv.bias.data = torch.tensor([0.0])
_conv.weight.data = torch.tensor([[[[1/9,1/9,1/9],[1/9,1/9,1/9],[1/9,1/9,1/9]]]])(3,3)이나~ 3이나~
_X,_conv(_X)(tensor([[[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.],
[15., 16., 17., 18., 19.],
[20., 21., 22., 23., 24.]]]]),
tensor([[[[ 6.0000, 7.0000, 8.0000],
[11.0000, 12.0000, 13.0000],
[16.0000, 17.0000, 18.0000]]]], grad_fn=<ThnnConv2DBackward0>))(1+2+3+6+7+8+11+12+13)/97.0(예시5) 피처뻥튀기
_X = torch.tensor([1.0,1.0,1.0,1.0]).reshape(1,1,2,2)
_Xtensor([[[[1., 1.],
[1., 1.]]]])_conv = torch.nn.Conv2d(1,8,(2,2))
_conv.weight.data.shape,_conv.bias.data.shape(torch.Size([8, 1, 2, 2]), torch.Size([8]))_conv(_X).shapetorch.Size([1, 8, 1, 1])_conv(_X).reshape(-1)tensor([-0.3464, 0.2739, 0.1069, 0.6105, 0.0432, 0.8390, 0.2353, 0.2345],
grad_fn=<ReshapeAliasBackward0>)torch.sum(_conv.weight.data[0,...])+_conv.bias.data[0],\
torch.sum(_conv.weight.data[1,...])+_conv.bias.data[1](tensor(-0.3464), tensor(0.2739))결국 아래를 계산한다는 의미
torch.sum(_conv.weight.data,axis=(2,3)).reshape(-1)+ _conv.bias.datatensor([-0.3464, 0.2739, 0.1069, 0.6105, 0.0432, 0.8390, 0.2353, 0.2345])_conv(_X).reshape(-1)tensor([-0.3464, 0.2739, 0.1069, 0.6105, 0.0432, 0.8390, 0.2353, 0.2345],
grad_fn=<ReshapeAliasBackward0>)(잔소리) axis 사용 익숙하지 않으면 아래 꼭 들으세요..
- https://guebin.github.io/IP2022/2022/04/11/(6주차)-4월11일.html , numpy공부 4단계: 축
ReLU (2d)
_X = torch.randn(25).reshape(1,5,5)
_Xtensor([[[ 0.2656, 0.0780, 3.0465, 1.0151, -2.3908],
[ 0.4749, 1.6519, 1.5454, 1.0376, 0.9291],
[-0.7858, 0.4190, 2.6057, -0.4022, 0.2092],
[ 0.9594, 0.6408, -0.0411, -1.0720, -2.0659],
[-0.0996, 1.1351, 0.9758, 0.4952, -0.5475]]])a1=torch.nn.ReLU()a1(_X)tensor([[[0.2656, 0.0780, 3.0465, 1.0151, 0.0000],
[0.4749, 1.6519, 1.5454, 1.0376, 0.9291],
[0.0000, 0.4190, 2.6057, 0.0000, 0.2092],
[0.9594, 0.6408, 0.0000, 0.0000, 0.0000],
[0.0000, 1.1351, 0.9758, 0.4952, 0.0000]]])Maxpooling 레이어
_maxpooling = torch.nn.MaxPool2d((2,2))_X = torch.arange(16).float().reshape(1,4,4) _X, _maxpooling(_X) (tensor([[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]]]),
tensor([[[ 5., 7.],
[13., 15.]]]))가장 중요한 특징만 남게 될 것이다.
_X = torch.arange(25).float().reshape(1,5,5) _X, _maxpooling(_X) (tensor([[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.],
[15., 16., 17., 18., 19.],
[20., 21., 22., 23., 24.]]]),
tensor([[[ 6., 8.],
[16., 18.]]]))버려지는 데이터
_X = torch.arange(36).float().reshape(1,6,6) _X, _maxpooling(_X) (tensor([[[ 0., 1., 2., 3., 4., 5.],
[ 6., 7., 8., 9., 10., 11.],
[12., 13., 14., 15., 16., 17.],
[18., 19., 20., 21., 22., 23.],
[24., 25., 26., 27., 28., 29.],
[30., 31., 32., 33., 34., 35.]]]),
tensor([[[ 7., 9., 11.],
[19., 21., 23.],
[31., 33., 35.]]]))이미지자료분석– CNN 구현 (CPU)
X.shapetorch.Size([12665, 1, 28, 28])(1) Conv2d
c1 = torch.nn.Conv2d(1,16,(5,5))
print(X.shape)
print(c1(X).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])(2) ReLU
a1 = torch.nn.ReLU()
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])(3) MaxPool2D
m1 = torch.nn.MaxPool2d((2,2))
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])(4) 적당히 마무리하고 시그모이드 태우자
- 펼치자.
(방법1)
m1(a1(c1(X))).reshape(-1,2304).shapetorch.Size([12665, 2304])16*12*12 2304(방법2)
flttn = torch.nn.Flatten()print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])- 2304 \(\to\) 1 로 차원축소하는 선형레이어를 설계
l1 = torch.nn.Linear(in_features=2304,out_features=1)
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)
print(l1(flttn(m1(a1(c1(X))))).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])
torch.Size([12665, 1])- 시그모이드
a2 = torch.nn.Sigmoid()l1 = torch.nn.Linear(in_features=2304,out_features=1)
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)
print(l1(flttn(m1(a1(c1(X))))).shape)
print(a1(l1(flttn(m1(a1(c1(X)))))).shape)torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])
torch.Size([12665, 1])
torch.Size([12665, 1])- 네트워크 설계
net = torch.nn.Sequential(
c1, # 2d: 컨볼루션(선형변환), 피처 뻥튀기
a1, # 2d: 렐루(비선형변환)
m1, # 2d: 맥스풀링: 데이터요약
flttn, # 2d->1d
l1, # 1d: 선형변환
a2 # 1d: 시그모이드(비선형변환)
)loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())t1= time.time()
for epoc in range(100):
## 1
yhat = net(X)
## 2
loss = loss_fn(yhat,y)
## 3
loss.backward()
## 4
optimizr.step()
optimizr.zero_grad()
t2= time.time()
t2-t139.31594634056091plt.plot(y)
plt.plot(net(X).data,'.')
plt.title('Traning Set',size=15)Text(0.5, 1.0, 'Traning Set')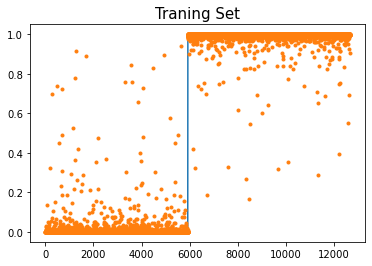
plt.plot(yy)
plt.plot(net(XX).data,'.')
plt.title('Test Set',size=15)Text(0.5, 1.0, 'Test Set')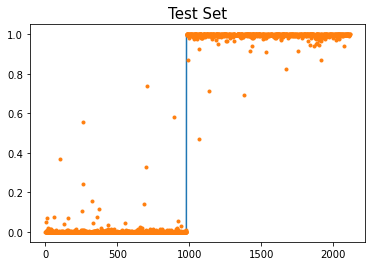
이미지자료분석– CNN 구현 (GPU)
1. dls
ds1=torch.utils.data.TensorDataset(X,y)
ds2=torch.utils.data.TensorDataset(XX,yy)X.shapetorch.Size([12665, 1, 28, 28])len(X)/101266.5len(XX)2115dl1 = torch.utils.data.DataLoader(ds1,batch_size=1266)
dl2 = torch.utils.data.DataLoader(ds2,batch_size=2115) dls = DataLoaders(dl1,dl2) # 이거 fastai 지원함수입니다2. lrnr 생성: 아키텍처, 손실함수, 옵티마이저
net = torch.nn.Sequential(
torch.nn.Conv2d(1,16,(5,5)),
torch.nn.ReLU(),
torch.nn.MaxPool2d((2,2)),
torch.nn.Flatten(),
torch.nn.Linear(2304,1),
torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()lrnr = Learner(dls,net,loss_fn)3. 학습
lrnr.fit(10) | epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.901239 | 0.605223 | 00:00 |
| 1 | 0.660227 | 0.370985 | 00:00 |
| 2 | 0.507106 | 0.213785 | 00:00 |
| 3 | 0.393017 | 0.113283 | 00:00 |
| 4 | 0.304846 | 0.065374 | 00:00 |
| 5 | 0.238648 | 0.042887 | 00:00 |
| 6 | 0.189261 | 0.031143 | 00:00 |
| 7 | 0.152003 | 0.024236 | 00:00 |
| 8 | 0.123435 | 0.019730 | 00:00 |
| 9 | 0.101176 | 0.016531 | 00:00 |
lrnr.modelSequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
(3): Flatten(start_dim=1, end_dim=-1)
(4): Linear(in_features=2304, out_features=1, bias=True)
(5): Sigmoid()
)4. 예측 및 시각화
net.to("cpu") Sequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
(3): Flatten(start_dim=1, end_dim=-1)
(4): Linear(in_features=2304, out_features=1, bias=True)
(5): Sigmoid()
)- 결과를 시각화하면 아래와 같다.
plt.plot(net(X).data,'.')
plt.title("Training Set",size=15)Text(0.5, 1.0, 'Training Set')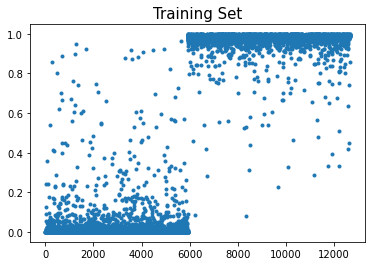
plt.plot(net(XX).data,'.')
plt.title("Test Set",size=15)Text(0.5, 1.0, 'Test Set')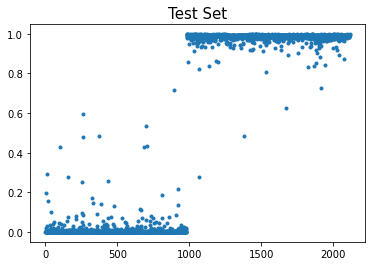
1/10만 사용했는데 잘 training된 것 같다
- 빠르고 적합결과도 좋음
Lrnr 오브젝트
lrnr.modelSequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
(3): Flatten(start_dim=1, end_dim=-1)
(4): Linear(in_features=2304, out_features=1, bias=True)
(5): Sigmoid()
)netSequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
(3): Flatten(start_dim=1, end_dim=-1)
(4): Linear(in_features=2304, out_features=1, bias=True)
(5): Sigmoid()
)id(lrnr.model), id(net)(140021490006720, 140021490006720)lrnr.model(X)tensor([[4.5555e-05],
[1.2910e-03],
[6.6828e-04],
...,
[9.8670e-01],
[9.8576e-01],
[9.9344e-01]], grad_fn=<SigmoidBackward0>)net(X)tensor([[4.5555e-05],
[1.2910e-03],
[6.6828e-04],
...,
[9.8670e-01],
[9.8576e-01],
[9.9344e-01]], grad_fn=<SigmoidBackward0>)같은 결과
20221026 수업
BCEWithLogitsLoss
- BCEWithLogitsLoss = Sigmoid + BCELoss - 왜 써요? 수치적으로 더 안정
torch.nn.BCEWithLogitsLoss - This loss combines a Sigmoid layer and the BCELoss in one single class. This version is more numerically stable than using a plain Sigmoid followed by a BCELoss as, by combining the operations into one layer, we take advantage of the log-sum-exp trick for numerical stability.
- 사용방법
- dls 만들기
ds1=torch.utils.data.TensorDataset(X,y)
ds2=torch.utils.data.TensorDataset(XX,yy)torch.utils.data.TensorDataset?Init signature: torch.utils.data.TensorDataset(*args, **kwds) Docstring: Dataset wrapping tensors. Each sample will be retrieved by indexing tensors along the first dimension. Args: *tensors (Tensor): tensors that have the same size of the first dimension. File: ~/anaconda3/envs/csy/lib/python3.8/site-packages/torch/utils/data/dataset.py Type: type Subclasses:
dl1 = torch.utils.data.DataLoader(ds1,batch_size=1266)
dl2 = torch.utils.data.DataLoader(ds2,batch_size=2115) dls = DataLoaders(dl1,dl2) # 이거 fastai 지원함수입니다- lrnr생성
net = torch.nn.Sequential(
torch.nn.Conv2d(1,16,(5,5)),
torch.nn.ReLU(),
torch.nn.MaxPool2d((2,2)),
torch.nn.Flatten(),
torch.nn.Linear(2304,1),
#torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCEWithLogitsLoss()
lrnr = Learner(dls,net,loss_fn) - 학습
lrnr.fit(10)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.956781 | 0.642780 | 00:00 |
| 1 | 0.709626 | 0.419758 | 00:00 |
| 2 | 0.554641 | 0.248010 | 00:00 |
| 3 | 0.431661 | 0.118707 | 00:00 |
| 4 | 0.331514 | 0.059536 | 00:00 |
| 5 | 0.256312 | 0.035956 | 00:00 |
| 6 | 0.200917 | 0.025288 | 00:00 |
| 7 | 0.159611 | 0.019510 | 00:00 |
| 8 | 0.128254 | 0.015889 | 00:00 |
| 9 | 0.104057 | 0.013373 | 00:00 |
- 예측 및 시각화
net.to("cpu")Sequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
(3): Flatten(start_dim=1, end_dim=-1)
(4): Linear(in_features=2304, out_features=1, bias=True)
)시각화 위해서 cpu로 옮겨주기
net(X)tensor([[-9.4061],
[-6.7910],
[-7.9819],
...,
[ 4.3685],
[ 4.4061],
[ 5.4793]], grad_fn=<AddmmBackward0>)sigmoid 취하기 전이지 우리는 bcewithlogiticsLoss 썼잖아, 그래서 0~1사이 아님
a2(torch.tensor(0))tensor(0.5000)fig,ax = plt.subplots(1,2,figsize=(8,4))
ax[0].plot(net(X).data,',',color="C1")
ax[1].plot(y)
ax[1].plot(a2(net(X)).data,',')
fig.suptitle("Training Set",size=15)Text(0.5, 0.98, 'Training Set')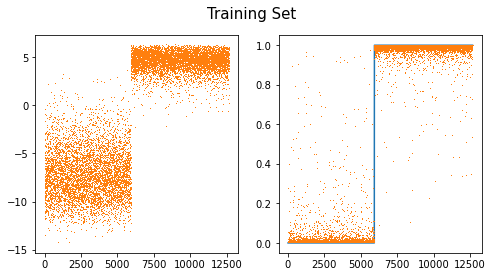
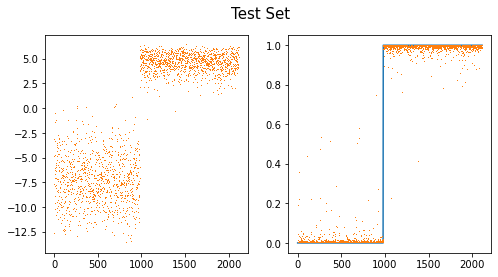
fig,ax = plt.subplots(1,2,figsize=(8,4))
ax[0].plot(net(XX).data,',',color="C1")
ax[1].plot(yy)
ax[1].plot(a2(net(XX)).data,',')
fig.suptitle("Test Set",size=15)Text(0.5, 0.98, 'Test Set')