import numpy as np
import matplotlib.pyplot as plt
import scipy14wk-1,2: MCMC (2)
2023-06-01
강의영상
youtube: https://youtube.com/playlist?list=PLQqh36zP38-zN7idmV8iVcOs4zV2Lg8WE
- 이 강의는 14wk-1, 14wk-2 의 강의가 합쳐져 있습니다.
imports
약간의 이론
- 이론: \(\{X_t\}\)가 IRR-HMC1 라고 하자.
- 만약에 \(\{X_t\}\)가 정상분포를 가진다면 그 정상분포는 유일한 정상분포이다.
- 1이 성립한다면 \(\{X_t\}\)는 positive recurrent HMC가 된다.2
- \(\{X_t\}\)는 IRR-PR-HMC 이므로 주기를 논의할 수 있다.3 만약에 \(\{X_t\}\)가 aperiodic 이면4 \(\{X_t\}\)는 에르고딕 마코프체인이 된다.
- 따라서 이 경우는 \(\bar{\boldsymbol \pi} \to {\boldsymbol \pi} = {\bf p}_{\star}\) 가 성립한다. (nice case)
- 무기: \(\{X_t\}\)가 IRR-HMC라고 할때 (1) 어떠한 방식으로든 정상분포가 존재함을 보이고 (유일함을 보이지 않더라도 유일해짐) (2) AP 임을 보이면 nice case가 된다.
사실상 periodicity는 \(\frac{1}{2}({\bf P} + {\bf I})\) 와 같은 방식으로 쉽게 kill 할 수 있으므로 “\(\exists {\boldsymbol \pi}\)”를 보이면 nice case 를 만들수 있다고 봐야함.
- Thm: \(\{X_t\}\)가 IRR-HMC라고 하고 \({\bf P}\) 가 \(\{X_t\}\)의 transition matrix (혹은 그 비슷한 것) 이라고 하자. 분포의 정의를 만족하는 어떠한 벡터 \({\boldsymbol \mu}\)가 아래의 조건을 만족한다면
\[\forall i,j \in E:~\mu_ip_{ij} = \mu_jp_{ji} \quad \quad \cdots (\star)\]
위에가 아래보다 강한 조건
벡터 \({\boldsymbol \mu}\)는 정상분포이다. 즉 아래가 성립한다.
\[{\boldsymbol \mu}^\top {\bf P} = {\boldsymbol \mu}^\top \quad \cdots (\star\star)\]
단 여기에서 편의상 아래와 같이 생각하자.
\({\boldsymbol \mu}^\top = [\mu_0,\mu_1,\dots]\)
\({\bf P} = \begin{bmatrix} p_{00} & p_{01} & \dots \\ p_{10} & p_{11} & \dots \\ \dots & \dots & \dots \end{bmatrix}\)
- 조건 \((\star)\)를 detailed balance condition (DBC) 라고 부른다. 이 조건은 정상분포가 존재할 조건 \((\star\star)\) 보다 강한조건이다. 즉 \((\star) \Rightarrow (\star\star)\) 이다.
\(\Rightarrow\)imply 한다고 표현, 위에서 반대는 안 됌!
- DBC가 \({\boldsymbol \mu}^\top {\bf P} = {\boldsymbol \mu}^\top\) 를 하는 이유를 체크하기 위해서 \((\star)\)의 양변에 \(\sum_i\)를 취하면 된다. 아래의 1,2,3을 관찰해볼 것.
- \(\forall j\in E:~ \sum_{i}\mu_i p_{ij} = \sum_{i} \mu_j p_{ji}\)
- \(\forall j\in E:~ \sum_{i}\mu_i p_{ij} = \mu_j\)
- \({\boldsymbol \mu}^\top {\bf P} = {\boldsymbol \mu}^\top\)
- (용어) DBC를 만족하는 마코프체인을 reversible 하다고 표현하다.
Toy Example
- 예시1: 아래와 같은 transitio matrix를 고려하자. (08wk-1에 소개된 예제)
P = np.array([[0.4,0.6],
[0.9,0.1]])
Parray([[0.4, 0.6],
[0.9, 0.1]])아래와 같은 벡터를 고려하자.
π = np.array([[0.6],[0.4]])
π.Tarray([[0.6, 0.4]])\({\boldsymbol \pi}\)가 DBC조건을 만족하는지 체크하자.5
# i=0, j=0
π[0]*P[0,0], π[0]*P[0,0](array([0.24]), array([0.24]))# i=0, j=1
π[0]*P[0,1], π[1]*P[1,0](array([0.36]), array([0.36]))# i=1, j=0
π[1]*P[1,0], π[0]*P[0,1](array([0.36]), array([0.36]))# i=1, j=1
π[1]*P[1,1], π[1]*P[1,1](array([0.04]), array([0.04]))DBC를 만족하므로 \({\boldsymbol \pi}\)는 정상분포이다. 또한 이 예제에서는 IRR조건이 만족하므로 이 정상분포는 유일해진다. 그리고 IRR이고 “\(\exists! {\boldsymbol \pi}\)” 이므로 이 마코프체인은 PR이다. 그리고 이 마코프체인은 AP이므로 결국에는 에르고딕 마코프체인이 된다.
- 샘플링: 아래와 같은 분포 \({\boldsymbol \pi}\)를 따르는 확률변수 \(X\)를 생성하고 싶다고 하자.
\(\exists!\) 정상분포이고 유일하다는 뜻
| \(X\) | \(0\) | \(1\) |
|---|---|---|
| \(\mathbb{P}(X=k)\) | \(0.6\) | \(0.4\) |
그렇다면 아래와 같은 \({\bf P}\)에서 계속 샘플링을 하면 된다.
Parray([[0.4, 0.6],
[0.9, 0.1]])def rain(before):
if before == 0:
after = np.random.rand() < 0.6
else:
after = np.random.rand() < 0.1
return after*1def doctor_strange(x0):
lst = [x0]
for t in range(10500):
lst.append(rain(lst[t]))
return lst xx = doctor_strange(0)plt.hist(xx[501:],bins=100);
- 샘플링이 성공하는 이유? (당연한 것 같은데 그래도 써보면)
아래와 같은 조건부확률에 따라 \(X\)에서 \(X'\)을 반복적으로 만들면
- \(p_{00} = \mathbb{P}(X'=0 | X=0)=0.4\)
- \(p_{01} = \mathbb{P}(X'=1 | X=0)=0.6\)
- \(p_{10} = \mathbb{P}(X'=0 | X=1)=0.9\)
- \(p_{11} = \mathbb{P}(X'=1 | X=1)=0.1\)
결국 \(X_{\infty}\)는 분포 \({\boldsymbol \pi}^\top = [0.6, 0.4]\)를 pmf로 가진다. 이러한 분포의 히스토그램은 원래
\[X_{\infty}(\omega_1),X_{\infty}(\omega_2),X_{\infty}(\omega_3),\dots\]
와 같은 샘플을 모아서 그려야 하지만
\[X_{T_0}(\omega_1),X_{T_0+1}(\omega_1),X_{T_0+2}(\omega_2),\dots\]
와 같은 샘플을 모아서 그릴 수 있다.6 여기에서 \(T_0\)는 적당히 큰 숫자이고 우리의 예제의 경우 \(T_0=500\)을 설정하였다.
- 주의: 물론 이 예제는 샘플링이 어렵지 않습니다. 아래와 같이 뽑아도 됩니다.
xx = (np.random.rand(10000) < 0.4)*1MCMC
샘플추천X & 이산형
- 모티브: 위의 예제에서 전이행렬이 꼭 아래와 같을 필요는 없는것 아닌가?
Parray([[0.4, 0.6],
[0.9, 0.1]])- 우리의 목표: 아래와 같은 분포 \({\boldsymbol \pi}\)를 따르는 확률변수 \(X\)를 생성하기만 하면 되는 것 아닌가?
| \(X\) | \(0\) | \(1\) |
|---|---|---|
| \(\mathbb{P}(X=k)\) | \(0.6\) | \(0.4\) |
이러한 정상분포를 가지는 에르고딕 마코프체인의 전이행렬 \({\bf P}\)를 역으로 설계해보자.
P = np.array([[0.6,0.4],
[0.6,0.4]])Parray([[0.6, 0.4],
[0.6, 0.4]])- DBC 체크: 아래의 detailed balance condition을 만족하기만 하면 target distribution \({\boldsymbol \pi}\)는 새롭게 설계한 \({\bf P}\)를 가지는 HMC \(\{X_t\}\)의 정상분포라 주장할 수 있다.
\[\forall i,j \in E:~ \pi_ip_{ij}=\pi_jp_{ji}\]
이 예제의 경우
\[\forall i,j \in E:~ \pi_i\pi_{j}=\pi_j\pi_{i}\]
가 되므로 성립한다.
- 따라서 전이행렬 \({\bf P}\)를 가지는 마코프체인은 \({\boldsymbol \pi}^\top=[0.4,0.6]\)를 정상분포로 가지는 마코프체인이다.7 이 마코프체인은 IRR 이므로 정상분포 \({\boldsymbol \pi}\)는 유일한 정상분포가 되고, 따라서 PR조건이 만족된다. 또한 AP를 만족하므로 에르고딕 마코프체인이 된다.
Parray([[0.6, 0.4],
[0.6, 0.4]])def doctor_strange(x0):
xx = [x0]
for t in range(10500):
_u = np.random.rand()
if _u < 0.4:
xx.append(1)
else:
xx.append(0)
return xx xx = doctor_strange(0)plt.hist(xx[501:],bins=100);
- 이러한 방식은 유한차원으로 확장가능하다. (그런데 귀찮다)
| \(X\) | \(0\) | \(1\) | \(2\) |
|---|---|---|---|
| \(\mathbb{P}(X=k)\) | \(0.6\) | \(0.2\) | \(0.2\) |
P = np.array([[0.6,0.2,0.2],
[0.6,0.2,0.2],
[0.6,0.2,0.2]])def doctor_strange(x0):
xx = [x0]
for t in range(10500):
_u = np.random.rand()
if _u < 0.6:
xx.append(0)
elif _u< 0.8:
xx.append(1)
else:
xx.append(2)
return xx xx = doctor_strange(0)plt.hist(xx[501:],bins=100);
샘플추천 & 이산형
- 아래의 분포를 고려하자.
np.random.seed(43052)
u = np.random.rand(10)
π = (u/u.sum()).reshape(-1,1)
π.Tarray([[0.12977311, 0.00786117, 0.13310662, 0.09836388, 0.01944822,
0.01858917, 0.13959302, 0.15544153, 0.14440391, 0.15341937]])plt.stem(π)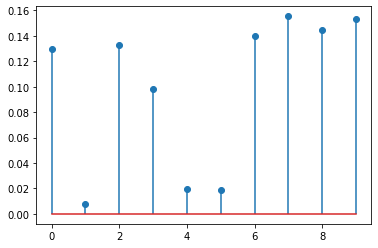
- 이러한 분포에서 샘플을 뽑는 상황을 고려하자.
- 위의 코드로는 못하겠다.
- 다른 방법은 없을까?
그냥 저번시간처럼 하자. \(x\)에서 \(x'\)으로 가는 확률을 다 정의하지 말고, \(x'\)를 적당히 추천받고 옮겨탈지 말지 결정하자.
- 저번시간 테크닉: \(X(\omega_1)=x\)가 주어졌을때 \(X'(\omega_1)=x'\)를 뽑는 방법!
- \(x\)가 주어졌다고 가정하자.
- \(x'\)의 후보로 \(Y(\omega^\ast)=y\)를 뽑는다. \(Y \sim {\boldsymbol p}_Y:=[\frac{1}{10},\dots,\frac{1}{10}]\)
- \(x'\)은 \(x\)가 적절한지, 아니면 추천받은 \(y\)가 적절한지 따져보고 결정한다. 즉 아래의 확률로 \(x'=y\)를 선택한다.
\[\frac{\pi_y}{\pi_x + \pi_y}\]
- 의문: 저렇게 막 만들어도 에르고딕한지 어떻게 알지?
- 당연히 몰라요.
- 조사를 좀 해봐야 합니다.
- DBC condition 체크
\[\forall i,j \in E:~ \pi_ip_{ij}=\pi_jp_{ji}\]
노테이션을 살짝 변경하면 아래와 같다.
\[\forall x,x' \in E:~ \pi_xp_{xx'}=\pi_{x'}p_{x'x}\]
여기에서 \(p_{xx'}\)와 \(p_{x'x}\)를 각각 구하면 아래와 같다.
\[p_{xx'} = \frac{1}{10}\frac{\pi_{x'}}{\pi_x + \pi_{x'}}\]
\[p_{x'x} = \frac{1}{10}\frac{\pi_{x}}{\pi_x + \pi_{x'}}\]
따라서 DBC가 성립한다.
- 이론전개: DBC가 만족되었으므로 \({\boldsymbol \pi}\)는 정상분포가 된다. 그리고 이 마코프체인은 IRR 이므로 정상분포는 유일해진다. 또한 IRR-HMC에서는 유일한 정상분포의 존재와 PR이 동치이므로 이 마코프체인은 PR이 된다. 또한 이 마코프체인은 AP조건을 만족한다. 따라서 이 마코프체인은 에르고딕이 된다.
def doctor_strange(x0):
xx = [x0]
for t in range(100500):
y = np.random.choice(range(10))
acceptance_prob = π[y]/(π[xx[t]]+π[y]) ## acceptance_prob 가 클수록 y가 선택
_u = np.random.rand()
if _u < acceptance_prob:
xx.append(y)
else:
xx.append(xx[t])
return xx xx = doctor_strange(0)plt.stem(π*100000)
plt.hist(xx[501:],bins=100,color='C1',alpha=0.8);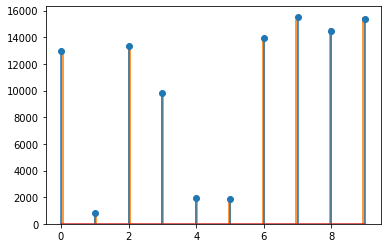
참고
### 비교를 위해 이전에 만들었던 코드를 확인해보자.
T = 100000
xx = [0.99]
for t in range(T):
y = np.random.rand()
thresh_prob = f(y)/(f(xx[t])+f(y)) ## thresh_prob 가 클수록 y가 선택
_u = np.random.rand()
if _u < thresh_prob:
xx.append(y)
else:
xx.append(xx[t])샘플추천 & 연속형
- 아래와 같은 pdf \(f_X(x)\)를 가지는 확률변수를 만들고 싶다면?
g = scipy.special.gammadef f(x):
return g(2+6)/(g(2)*g(6)) * x**(2-1) * (1-x)**(6-1)_x = np.linspace(0,1,1000)
plt.plot(_x, f(_x))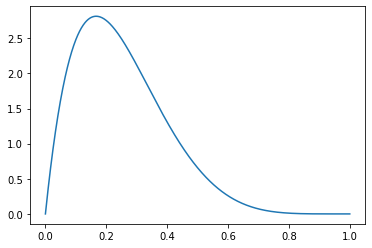
- 어? 잠깐만..
- 이전예제: \(E= \{0,1,2,3,4,5,6,7,8,9\}\)
- 지금예제: \(E= [0,1]\)
상태공간 \(E\) coutable 이 아니잖아? (그래도 일단 진행해보자)
- 테크닉: \(X(\omega_1)=x\)가 주어졌을때 \(X'(\omega_1)=x'\)를 뽑는 방법!
- \(x\)가 주어졌다고 가정하자.
- \(x'\)의 후보로 \(Y(\omega^\ast)=y\)를 뽑는다. \(Y \sim {\cal U}\)
- \(x'\)은 \(x\)가 적절한지, 아니면 추천받은 \(y\)가 적절한지 따져보고 결정한다. 즉 아래의 확률로 \(x'=y\)를 선택한다.
\[\frac{f_X(y)}{f_X(x) + f_X(y)}\]
- DBC condition 체크
이전예제
\[\forall x,x' \in E:~ \pi_xp_{xx'}=\pi_{x'}p_{x'x}\]
지금예제
\[\forall x,x' \in E:~ f_X(x)p_{xx'}=f_X(x')p_{x'x}\]
여기에서 \(p_{xx'}\)와 \(p_{x'x}\)는 대충 아래와 같이 쓸 수 있을것 같다.
\[p_{xx'} = f_Y(x')\frac{f_X(x')}{f_X(x) + f_X(x')}\]
\[p_{x'x} = f_Y(x)\frac{f_X(x)}{f_X(x) + f_X(x')}\]
우선 \(f_Y(x')=f_Y(x)=1\) 이므로 지금까지의 논의가 맞다면 DBC는 만족된다.
- 의문1: 좀 이상한데? \(f_X(x)\)는 \(\pi_x\)와 다르게 확률을 의미하는게 아니잖아?
- 의문2: 애초에 HMC \(\{X_t\}\)를 coutable한 state space를 가진다고 정의하지 않았어?
Polish space
- MCMC 샘플링이 성공하는 이유를 다시 생각해보자.
아래와 같은 조건부확률에 따라 \(X\)에서 \(X'\)을 반복적으로 만들면
- \(p_{00} = \mathbb{P}(X'=0 | X=0)=0.4\)
- \(p_{01} = \mathbb{P}(X'=1 | X=0)=0.6\)
- \(p_{10} = \mathbb{P}(X'=0 | X=1)=0.9\)
- \(p_{11} = \mathbb{P}(X'=1 | X=1)=0.1\)
…. 중략
- 그런데 조건부 “확률”은 잘 정의할 수 있나?
- 할 수 있음.
- 상태공간이 \(E\)가 countable 일 경우에는 좀 쉬운편입니다. 그리고 조건부확률들을 모아서 매트릭스 (혹은 그 비슷한것) \({\bf P}\)를 만들수 있음.
- 상태공간이 \(E\)가 uncoutable 일 경우에는 좀 까다로운데 polish space라는 곳에서는 잘 정의됨. 그리고 조건부확률들을 모아서 매트릭스 (혹은 그 비슷한것) \({\bf P}\)를 만들 수는 없지만 대신에 transition kernel 이라는 것은 정의할 수 있습니다.
- 좀 더 이론적인건 엄밀하게 따져야하지만 (대학원외의 과정, 개인적으로 공부하고 싶으면 공부하는 영역임) 하여튼 연속형일 경우에도 가능합니다.
아무튼 연속형일 경우도 이산형처럼 가능하다.
- 앞으로는 연속형일지라도 이산형처럼 생각해서 논리전개하세요.
메트로폴리스-헤이스팅스
- 이전의 테크닉: \(X(\omega_1)=x\)가 주어졌을때 \(X'(\omega_1)=x'\)를 뽑는 방법!
- \(x\)가 주어졌다고 가정하자.
- \(x'\)의 후보로 \(Y(\omega^\ast)=y\)를 뽑는다. \(Y \sim {\boldsymbol p}_Y:=[\frac{1}{10},\dots,\frac{1}{10}]\)
- \(x'\)은 \(x\)가 적절한지, 아니면 추천받은 \(y\)가 적절한지 따져보고 결정한다. 즉 아래의 확률로 \(x'=y\)를 선택한다.
\[{\tt acceptance ~prob} =\frac{\pi_y}{\pi_x + \pi_y}\]
- 새로운 테크닉: \(X(\omega_1)=x\)가 주어졌을때 \(X'(\omega_1)=x'\)를 뽑는 방법!
- \(x\)가 주어졌다고 가정하자.
- \(x'\)의 후보로 \(Y(\omega^\ast)=y\)를 뽑는다. \(Y \sim {\boldsymbol p}_Y:=[\frac{1}{10},\dots,\frac{1}{10}]\)
- \(x'\)은 \(x\)가 적절한지, 아니면 추천받은 \(y\)가 적절한지 따져보고 결정한다. 즉 아래의 확률로 \(x'=y\)를 선택한다.
\[{\tt acceptance ~prob} =\min\left(1,\frac{\pi_y}{\pi_x}\right)\]
- DBC를 만족하는지 체크
\[\forall x,x' \in E:~ \pi_xp_{xx'}=\pi_{x'}p_{x'x}\]
여기에서 \(p_{xx'}\)와 \(p_{x'x}\)를 각각 구하면 아래와 같다.
\[p_{xx'} = \frac{1}{10}\min\left(1,\frac{\pi_{x'}}{\pi_x}\right)\]
\[p_{xx'} = \frac{1}{10}\min\left(1,\frac{\pi_{x}}{\pi_{x'}}\right)\]
경우를 (1) \(\pi_{x'} > \pi_x\) (2) \(\pi_{x'} < \pi_x\) 와 같이 나누어 풀어보면 DBC를 만족함을 쉽게 체크할 수 있다. 이후에 위의 예제들과 동일한 논리전개를 따르면 \(\{X_t\}\) 가 에르고딕 마코프체인임을 보일 수 있다. 따라서 새로운 테크닉으로 샘플을 뽑아도 무방하다.
Footnotes
irreducible 한 homogeneous markov chain↩︎
IRR-HMC 에서는 PR 조건과 \(\exists! {\boldsymbol \pi}\) 조건이 동치이므로.↩︎
주기를 논의할 수 있는 이유는 모든 상태가 recurrent 하므로.↩︎
즉 모든 상태에 대한 주기가 1이라면.↩︎
아직은 \({\boldsymbol \pi}\)가 정상분포인것은 모르지만 만약에 DBC를 만족하면 \({\boldsymbol \pi}\)를 정상분포라고 주장할 수 있음↩︎
\(X_{T_0}(\omega_1),X_{T_0+1}(\omega_1),X_{T_0+2}(\omega_2),\dots\) 는 동일한 분포를 가짐↩︎
DBC를 만족하기 때문에↩︎