Regression HW 4

고급회귀분석 과제, CH13

네 번째 과제입니다.

제출 기한 12월 8일

행렬 계산은 R로 해도 됩니다.

그리고, 계산 후에 R 함수(예:lm)를 이용하여 결과 확인하고, 본인의 풀이가 맞는지 결과 확인해보세요.

제출 방법

• 직접 제출(607호) 도 가능하지만,

• 문서 작성 후 pdf로 변환(★★★)하여 lms에 제출을 추천

(pdf 아닌 문서는 미제출로 간주)

• ★★★ 파일이름 : 이름(학번)_HW04.pdf

주의사항

• pdf로 꼭 변환하여 제출

• 풀이가 꼭 있어야 함 (답만 적혀 있는 경우 ’0’점 처리)

• 부정행위 시 ’F’학점

• 계산은 R로 해도 되지만 계산 풀이 과정이 꼭 있어야 함(수업 시간에 배운 식으로 풀이를 적어야 함.)!!

• lm등의 함수를 이용한 풀이는 정답 확인용으로만 사용.

---

library(ggplot2)

1.

일련번호	\(y\)(총 소요시간)	\(x_1\)(적성검사점수)	\(x_2\)(성별)	학력
1	17	151	남자	대
2	26	92	남자	고
3	21	175	남자	대
4	30	31	남자	고
5	22	104	남자	고
6	1	277	남자	대학원
7	12	210	남자	대학원
8	19	120	남자	대
9	4	290	남자	대학원
10	16	238	남자	대학원
11	28	164	여자	대학원
12	15	272	여자	대학원
13	11	295	여자	대학원
14	38	68	여자	고
15	31	85	여자	대
16	21	224	여자	대학원
17	20	166	여자	대
18	13	305	여자	대학원
19	30	124	여자	대
20	14	246	여자	대학원

df <- data.frame('y'=c(17,26,21,30,22,1,12,19,4,16,28,15,11,38,31,21,20,13,30,14),
           'x1'=c(151,92,175,31,104,277,210,120,290,238,164,272,295,68,85,224,166,305,124,246),
          'x2'=c('남자','남자','남자','남자','남자','남자','남자','남자','남자','남자','여자','여자','여자','여자','여자','여자','여자','여자','여자','여자'),
          'edu'=c('대','고','대','고','고','대학원','대학원','대','대학원','대학원','대학원','대학원','대학원','고','대','대학원','대','대학원','대','대학원'))

(1)

\(x_1\)을 \(x\)로 놓고 각 성별에 대하여 회귀모형을 적합하시오. 그런 후 두 회귀직선의 기울기가 같은지에 대한 가설검정을 하시오(5장 p12 : 두 회귀모형의 검정 참고).

answer

ggplot(df, aes(x1, y, col=x2)) + 
  geom_point() + 
  theme_bw() +
  guides(col=guide_legend(title="성별")) +
  scale_color_manual(labels = c("남자", "여자"), 
                     values = c("darkorange", "steelblue"))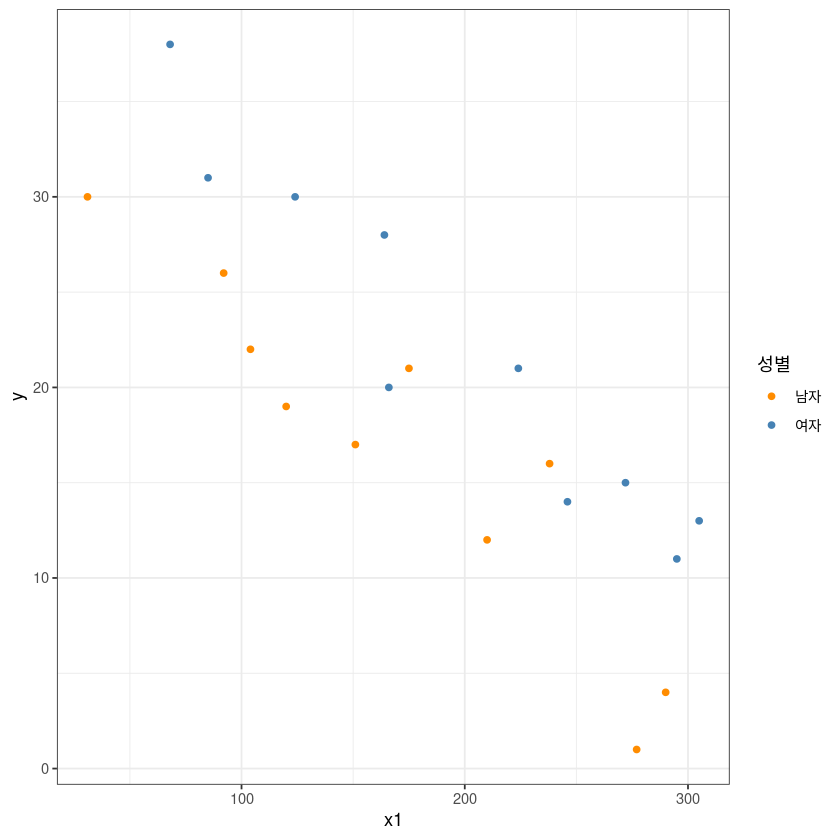

남성, Model 1: \(y_i = \beta_{01} + \beta_{11} x_{i1} + \epsilon_i , \epsilon_i \sim i.i.d. N(0, \sigma^2)\)

여성, Model 2: \(y_i = \beta_{02} + \beta_{12} x_{i2} + \epsilon_i , \epsilon_i \sim i.i.d. N(0, \sigma^2)\)

남자

plot(df$x1[df$x2=="남자"], df$y[df$x2=="남자"])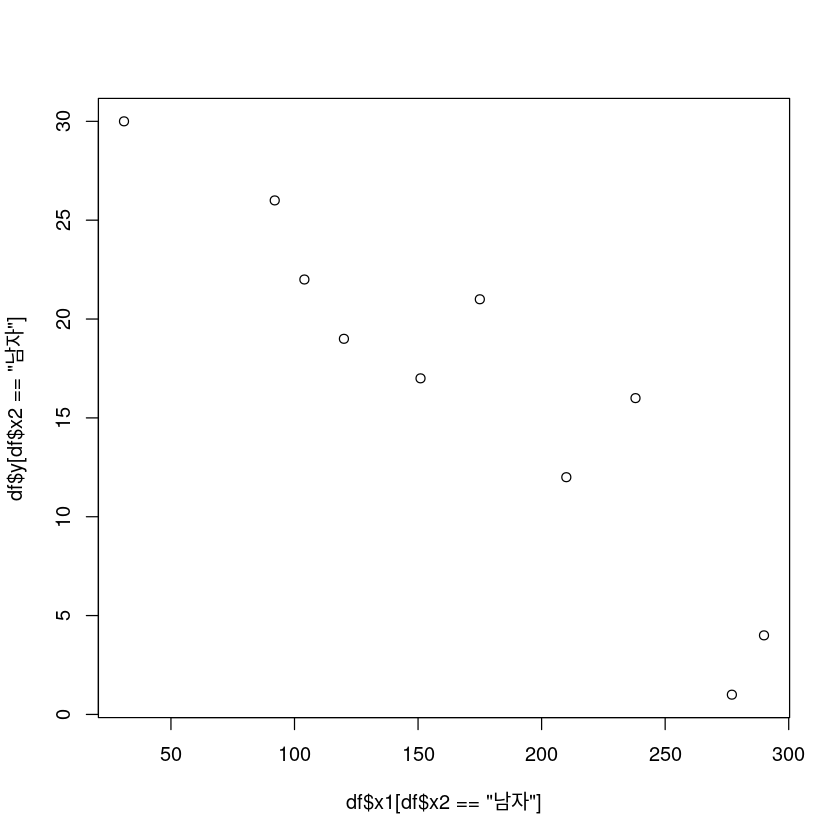

\(S_{yy}\)

sum((df$y[df$x2=="남자"] - (17+26+21+30+22+1+12+19+4+16)/10)**2)

745.6

\(S_{xx}\)

sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2)

64705.6

\(S_{xy}\)

sum((df$y[df$x2=="남자"] - (17+26+21+30+22+1+12+19+4+16)/10) * 
    (df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10))

-6461.4

\(\hat{\beta}_1 = \frac{S_{xy}}{S_{xx}}\)

beta_men <- round(sum((df$y[df$x2=="남자"] - (17+26+21+30+22+1+12+19+4+16)/10) *
    (df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)) / 
    sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2),5)
beta_men

-0.09986

\(\hat{\beta_0}\)

round((17+26+21+30+22+1+12+19+4+16)/10 - 
    round(sum((df$y[df$x2=="남자"] - (17+26+21+30+22+1+12+19+4+16)/10) *
    (df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)) / 
    sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2),5)*
    (151+92+175+31+104+277+210+120+290+238)/10,5)

33.65637

\(\hat{y}_{men} = 33.65637 -0.09986 x_{men}\)

---

R code

summary(lm(df$y[df$x2=="남자"]~df$x1[df$x2=="남자"]))

Call:
lm(formula = df$y[df$x2 == "남자"] ~ df$x1[df$x2 == "남자"])

Residuals:
    Min      1Q  Median      3Q     Max 
-4.9953 -1.5008 -0.6915  1.0080  6.1102 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)            33.65610    2.60379  12.926 1.21e-06 ***
df$x1[df$x2 == "남자"] -0.09986    0.01393  -7.171 9.51e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.542 on 8 degrees of freedom
Multiple R-squared:  0.8654,    Adjusted R-squared:  0.8485 
F-statistic: 51.43 on 1 and 8 DF,  p-value: 9.51e-05

---

answer

\(SSE_{men}\)

SSE_men <- sum((df$y[df$x2=="남자"] - (33.65637 - 0.09986*df$x1[df$x2=="남자"]))**2)
SSE_men

100.3747034298

\(MSE_{men} \sim \sigma^2_{men}\)

MSE_men <- sum((df$y[df$x2=="남자"] - (33.65637 - 0.09986*df$x1[df$x2=="남자"]))**2)/(10-2)
MSE_men

12.546837928725

---

R code

anova(lm(df$y[df$x2=="남자"]~df$x1[df$x2=="남자"]))

A anova: 2 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
df$x1[df$x2 == "남자"]	1	645.2253	645.22530	51.42533	9.509826e-05
Residuals	8	100.3747	12.54684	NA	NA

---

answer

여자

plot(df$x1[df$x2=="여자"], df$y[df$x2=="여자"])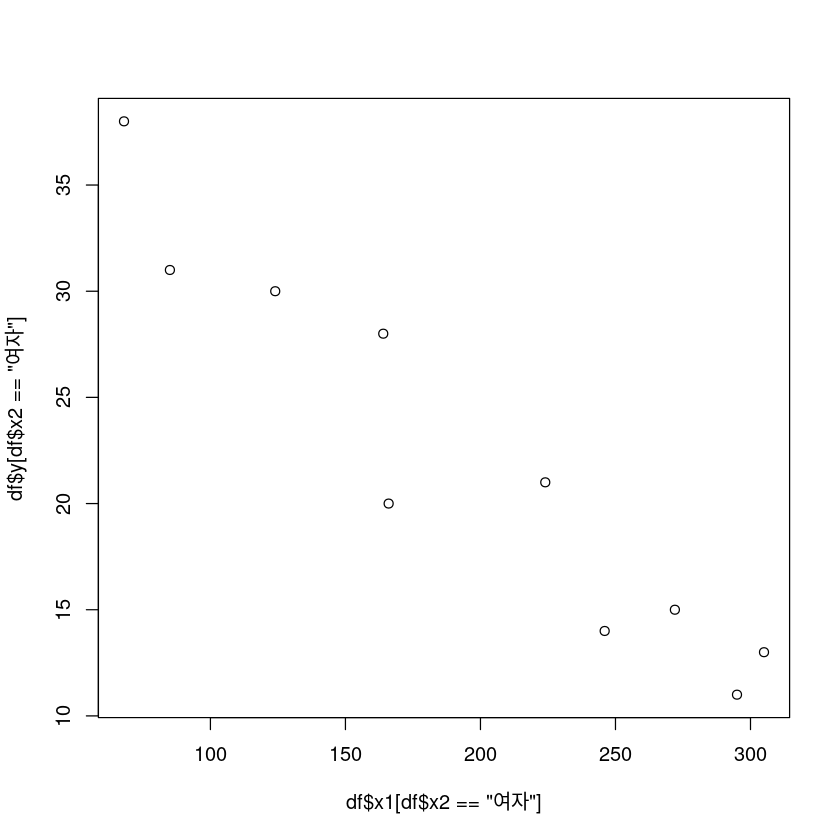

\(S_{yy}\)

sum((df$y[df$x2=="여자"] - (28+15+11+38+31+21+20+13+30+14)/10)**2)

756.9

\(S_{xx}\)

sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2)

66542.9

\(S_{xy}\)

sum((df$y[df$x2=="여자"] - (28+15+11+38+31+21+20+13+30+14)/10) * 
    (df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10))

-6783.9

\(\hat{\beta}_1 = \frac{S_{xy}}{S_{xx}}\)

beta_women <- round(sum((df$y[df$x2=="여자"] - (28+15+11+38+31+21+20+13+30+14)/10) * 
    (df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10))/
      sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2),5)
beta_women

-0.10195

\(\hat{\beta_0}\)

round((28+15+11+38+31+21+20+13+30+14)/10 - 
      round(sum((df$y[df$x2=="여자"] - (28+15+11+38+31+21+20+13+30+14)/10) * 
    (df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10))/
      sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2),5)*
      (164+272+295+68+85+224+166+305+124+246)/10,5)

41.97006

\(\hat{y}_{women} = 41.97006 -0.10195 x_{women}\)

---

R code

summary(lm(df$y[df$x2=="여자"]~df$x1[df$x2=="여자"]))

Call:
lm(formula = df$y[df$x2 == "여자"] ~ df$x1[df$x2 == "여자"])

Residuals:
   Min     1Q Median     3Q    Max 
-5.046 -1.952  0.716  2.060  2.963 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)            41.96962    2.33998  17.936 9.57e-08 ***
df$x1[df$x2 == "여자"] -0.10195    0.01108  -9.205 1.57e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.857 on 8 degrees of freedom
Multiple R-squared:  0.9137,    Adjusted R-squared:  0.9029 
F-statistic: 84.73 on 1 and 8 DF,  p-value: 1.57e-05

---

answer

\(SSE_{women}\)

SSE_women <- sum((df$y[df$x2=="여자"] - (41.97006 - 0.10195*df$x1[df$x2=="여자"]))**2)
SSE_women

65.2965503775

\(MSE_{women} \sim \sigma^2_{women}\)

MSE_women <- sum((df$y[df$x2=="여자"] - (41.97006 - 0.10195*df$x1[df$x2=="여자"]))**2)/(10-2)
MSE_women

8.1620687971875

---

R code

anova(lm(df$y[df$x2=="여자"]~df$x1[df$x2=="여자"]))

A anova: 2 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
df$x1[df$x2 == "여자"]	1	691.60345	691.603450	84.73384	1.56975e-05
Residuals	8	65.29655	8.162069	NA	NA

---

answer

가설

\(H_0: \beta_{11} - \beta_{12} = 0\)

\(H_0: \beta_{11} - \beta_{12} \neq 0\)

검정통계량 \(t_0 = \frac{\hat{\beta}_{11}- \hat{\beta}_{12}}{\sqrt{\hat{var}(\hat{\beta}_{11} - \hat{\beta}_{12})}}\sim H_0, t(n_1 - n_2 - 4)\)

\(var(\hat{\beta}_{11} - \hat{\beta}_{12})\)

\(= var(\hat{\beta}_{11}) + var(\hat{\beta}_{12})\)

\(= \frac{\sigma^2}{\sum(x_{11} - \bar{x}_{11})^2} + \frac{\sigma^2}{\sum(x_{12} - \bar{x}_{12})^2}\)

\(\hat{\beta}_{11} - \hat{\beta}_{12}\)

beta_men # CH13, p14 beta_1과 동일
beta_women # CH13 p1.4 beta1 + beta3 과 동일
# beta11 - beta12 = \beta3 = 0.0021

-0.09986

-0.10195

beta_men - beta_women

0.00208999999999999

\(\sigma^2 = MSE(FM) = \frac{SSE_{FM}}{n_1 + n_2 - 1}\)

\(\star SSE_{FM} = SSE_1 + SSE_2\)

SSE_men
SSE_women
SSE_men + SSE_women # SSE_FM
(SSE_men + SSE_women)/(10 +10-2)

100.3747034298

65.2965503775

165.6712538073

9.20395854485

\(\sqrt{var(\hat{\beta}_{11} - \hat{\beta}_{12}))}\)

sqrt(MSE_men/sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2) + 
    MSE_women/sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2))
# CG13 p,16 hat{=(s.e.)(beta_3)과 동일

0.0177922812236426

\(t_0\)

(beta_men - beta_women)/ 
    sqrt(MSE_men/sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2) + 
    MSE_women/sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2))

0.117466668479969

\(var(\hat{\beta}_{men} - \hat{\beta}_{women})\)

MSE_men/sum((df$x1[df$x2=="남자"] - (151+92+175+31+104+277+210+120+290+238)/10)**2) + 
    MSE_women/sum((df$x1[df$x2=="여자"] - (164+272+295+68+85+224+166+305+124+246)/10)**2)

0.000316565271141184

qt(0.025,16)

-2.11990529922126

기각역 : \(|t_0| > t_{\alpha/2}(n_1 + n_2 - 4) = 2.120\)

결론: 기각역에 속하지 않으므로 귀무가설 기각 못함.

\(H_0: \beta_{11} - \beta_{12} = 0\) 채택

따라서 성별간 두 기울기가 다르다고 할 수 없다.

---

R code

ggplot(df, aes(x1, y, col=x2)) + 
  geom_point() + 
  theme_bw() + 
  geom_abline(slope = coef(lm(df$y~df$x1*df$x2))[2], intercept = coef(lm(df$y~df$x1*df$x2))[1], col= 'darkorange')+
  geom_abline(slope = coef(lm(df$y~df$x1*df$x2))[2], intercept = coef(lm(df$y~df$x1*df$x2))[1]+coef(lm(df$y~df$x1*df$x2))[3], col= 'steelblue')+
  guides(col=guide_legend(title="성별")) +
  scale_color_manual(labels = c("남자", "여자"), values = c("darkorange", "steelblue"))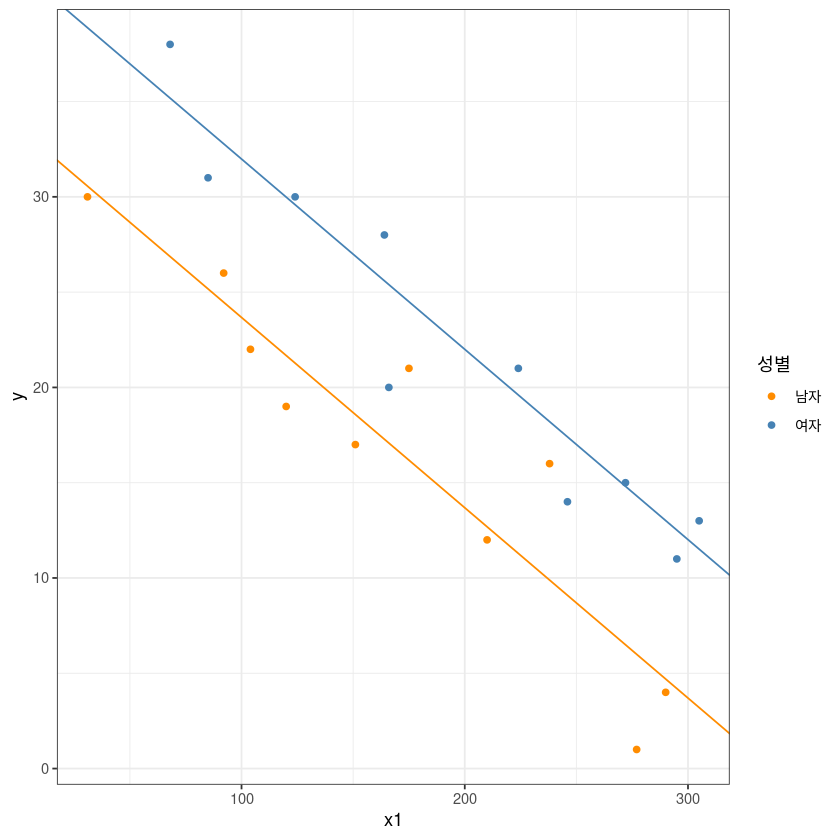

summary(lm(df$y~df$x1*df$x2))

Call:
lm(formula = df$y ~ df$x1 * df$x2)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.0463 -1.7591 -0.6232  1.9311  6.1102 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)     33.656104   2.365392  14.229 1.68e-10 ***
df$x1           -0.099858   0.012650  -7.894 6.59e-07 ***
df$x2여자        8.313516   3.541379   2.348   0.0321 *  
df$x1:df$x2여자 -0.002089   0.017766  -0.118   0.9078    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.218 on 16 degrees of freedom
Multiple R-squared:  0.8992,    Adjusted R-squared:  0.8803 
F-statistic: 47.56 on 3 and 16 DF,  p-value: 3.405e-08

\(\beta_3 = -0.002089\), 유의확률 $0.9078 $ 유의수준 \(\alpha=0.05\)에서 기각할 수 없다.

기각역: \(|t_0|?t_{\alpha/2}(n_1 + n_2 - 4) = t_{0.025}(16) = 2.120\)

기각역에 속하지 않으므로 \(H_0\) 기각 못함 \(H_0: \beta_{11} - \beta_{12} = 0\) 채택

따라서 성별간 두 기울기가 다르다고 할 수 없다.

(2)

13장 강의노트 p.8 에 따르면 \(x_1,x_2\)을 설명변수로 했을 때 적합 결과는 \[\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2\] \[= 33.8349 − 0.1009x_1 + 7.9340x_2\] 이었다. \(\beta_1\) 의 추정값 \(\hat{\beta}_1\) 이 갖는 분산을 추정하고, \(\beta_1\) 의 95% 신뢰구간을 구하시오.

answer

betahat_2 <- solve(t(matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3))%*%
      matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3))%*%
        t(matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3))%*%
        matrix(df$y,nrow=20,ncol=1)
betahat_2

A matrix: 3 × 1 of type dbl

33.8349119

-0.1009177

7.9339526

df$sex <- ifelse(df$x2=='여자',1,0)

\(var(\beta_1) = (x^\top x)^{-1}_{(2,2)} \sigma^2\)

t(matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3))%*%matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3)

A matrix: 3 × 3 of type dbl

20	3637	10
3637	796043	1949
10	1949	10

solve(t(matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3))%*%matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3))

A matrix: 3 × 3 of type dbl

0.31709536	-1.286110e-03	-0.0664325307
-0.00128611	7.619135e-06	-0.0001988594
-0.06643253	-1.988594e-04	0.2051902307

\((x^\top x)^{-1}_{(2,2)}\)

solve(t(matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3))%*%matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3))[2,2]

7.61913469487271e-06

\(MSE \sim \sigma^2\)

sum((matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3)%*%betahat_2 - df$y)**2)/17

9.75379176770424

\(var(\beta_1) = (x^\top x)^{-1}_{(2,2)} \sigma^2\)

hat_var_b1 <- ((solve(t(matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3)) %*% matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3)))[2,2])*
    sum((matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3)%*%betahat_2 - df$y)**2)/17
hat_var_b1

7.43154532638791e-05

sqrt(hat_var_b1)

0.00862064111675455

\(\beta_1 \pm t_{0.975}(17) se(\hat{\beta}_1)\)

betahat_2[2] - qt(0.975,17) * sqrt(hat_var_b1)

-0.119105687693037

betahat_2[2] + qt(0.975,17) * sqrt(hat_var_b1)

-0.0827297618549584

---

R code

summary(lm(df$y~matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3)))$coefficients

A matrix: 3 × 4 of type dbl

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	33.8349119	1.758659173	19.239039	5.635999e-13
matrix(c(rep(1, 20), df$x1, df$sex), nrow = 20, ncol = 3)2	-0.1009177	0.008620641	-11.706522	1.468240e-09
matrix(c(rep(1, 20), df$x1, df$sex), nrow = 20, ncol = 3)3	7.9339526	1.414702366	5.608213	3.134533e-05

anova(lm(df$y~matrix(c(rep(1,20),df$x1,df$sex),nrow=20,ncol=3)))

A anova: 2 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
matrix(c(rep(1, 20), df$x1, df$sex), nrow = 20, ncol = 3)	2	1477.1355	738.567770	75.72109	3.419664e-09
Residuals	17	165.8145	9.753792	NA	NA

confint(lm(df$y~matrix(c(rep(1,20),df$x1,rep(0,10),rep(1,10)),nrow=20,ncol=3)), level=0.95)

A matrix: 4 × 2 of type dbl

	2.5 %	97.5 %
(Intercept)	30.1244654	37.54535846
matrix(c(rep(1, 20), df$x1, rep(0, 10), rep(1, 10)), nrow = 20, ncol = 3)1	NA	NA
matrix(c(rep(1, 20), df$x1, rep(0, 10), rep(1, 10)), nrow = 20, ncol = 3)2	-0.1191057	-0.08272976
matrix(c(rep(1, 20), df$x1, rep(0, 10), rep(1, 10)), nrow = 20, ncol = 3)3	4.9491915	10.91871371

(3)

다음의 모형을 적합하시오. \[y_i =\beta_0 +\beta_1x_{1i} +\beta_2x_{2i} +\beta_3x_{3i} +\beta_4x_{4i} + \epsilon_i\]

\[x_{3i}=\begin{cases} 1: & \text{학력이 고졸} \\ 0 : &\text{기타} \end{cases}, x_{4i}= \begin{cases} 1 : & \text{학력이 대졸} \\ 0 : & \text{기타}\end{cases} \]

answer

df$high <- ifelse(df$edu=='고',1,0)

df$univ <- ifelse(df$edu=='대',1,0)

\(\hat{\beta}\)

x_hu <- matrix(c(rep(c(1),20),df$x1,df$sex,df$high,df$univ),nrow=20,ncol=5)

betahat_hu <- solve(t(x_hu)%*%x_hu)%*%t(x_hu)%*%df$y
betahat_hu

A matrix: 5 × 1 of type dbl

36.5226684

-0.1101234

7.8990531

-1.3758336

-2.4036479

\(y = 36.5226684 - 0.1101234 x_1 + 7.8990531 x_2 - 1.3758336 x_3 - 2.4036479 x_4\)

---

R code

summary(lm(y~x1+sex+high+univ,df))

Call:
lm(formula = y ~ x1 + sex + high + univ, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.0185 -1.7038 -0.5386  1.6375  6.1526 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 36.52267    5.33138   6.851 5.50e-06 ***
x1          -0.11012    0.01997  -5.516 5.93e-05 ***
sex          7.89905    1.50447   5.250 9.79e-05 ***
high        -1.37583    4.13333  -0.333    0.744    
univ        -2.40365    2.85796  -0.841    0.414    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.214 on 15 degrees of freedom
Multiple R-squared:  0.9057,    Adjusted R-squared:  0.8806 
F-statistic: 36.02 on 4 and 15 DF,  p-value: 1.587e-07

---

(4)

위의 모형에서 \(\beta_3\)과 \(\beta_4\)가 갖는 의미를 해석하시오.

\[y_i =\beta_0 +\beta_1x_{1i} +\beta_2x_{2i} +\beta_3x_{3i} +\beta_4x_{4i} + \epsilon_i\]

\[x_{3i}=\begin{cases} 1: & \text{학력이 고졸} \\ 0 : &\text{기타} \end{cases}, x_{4i}= \begin{cases} 1 : & \text{학력이 대졸} \\ 0 : & \text{기타}\end{cases} \]

answer

\(E(y) = \beta_0 +\beta_1x_{1} +\beta_2x_{2} +\beta_3x_{3} +\beta_4x_{4}\)

학력이 고등학교 졸업

\(E(y|고) = (\beta_0 +\beta_3) +\beta_1x_{1} +\beta_2x_{2}\)

학력이 대학교 졸업

\(E(y|고) = (\beta_0 +\beta_4)+\beta_1x_{1}+\beta_2x_{2}\)

학력이 대학원 졸업

\(E(y|대학원) = \beta_0 +\beta_1x_{1}+\beta_2x_{2}\)

\(\beta_3\) = 학력이 고등학교 졸업일때의 평균 숙련 시간에서 학력이 대학원 졸업일때의 평균 숙련시간을 뺀 값이다.

\(\beta_4\) = 학력이 대학교 졸업일때의 평균 숙련 시간에서 학력이 대학원 졸업일때의 평균 숙련시간을 뺀 값이다.

(5)

위의 \(\beta_3\)과 \(\beta_4\)의 최소제곱추정값 \(\hat{\beta}_3\)과 $_4$가 갖는 각각의 분산을 추정하시오. \(\beta_3\)과 \(\beta_4\)의 95% 신뢰구간을 구하시오

answer

\(var(\beta_3) = (x^\top x)^{-1}_{(4,4)} \sigma^2\)

t(x_hu)%*%x_hu

A matrix: 5 × 5 of type dbl

20	3637	10	4	6
3637	796043	1949	295	821
10	1949	10	1	3
4	295	1	4	0
6	821	3	0	6

solve(t(x_hu)%*%x_hu)

A matrix: 5 × 5 of type dbl

2.751920464	-0.009968093	-0.231607148	-1.958871839	-1.272149536
-0.009968093	0.000038595	0.000397155	0.007022423	0.004488433
-0.231607148	0.000397155	0.219140617	0.147531812	0.067692796
-1.958871839	0.007022423	0.147531812	1.654085215	0.924204433
-1.272149536	0.004488433	0.067692796	0.924204433	0.790802611

\((x^\top x)^{-1}_{(4,4)}\)

solve(t(x_hu)%*%x_hu)[4,4]

1.65408521513359

\(MSE \sim \sigma^2\)

sum((x_hu%*%betahat_hu - df$y)**2)

154.929453525913

sum((x_hu%*%betahat_hu - df$y)**2)/15

10.3286302350608

\(var(\hat{\beta}_3) = (x^\top x)^{-1}_{(4,4)} \sigma^2\)

hat_var_hu_b3 <- (solve(t(x_hu)%*%x_hu)[4,4]%*% sum((x_hu%*%betahat_hu - df$y)**2)/15)[,]
hat_var_hu_b3

17.0844345643959

sqrt(hat_var_hu_b3)

4.133332138166

\(t_{\alpha/2}(n-4-1)\)

qt(0.975,15)

2.13144954555978

\(\beta_3 \pm t_{0.975}(15) se(\hat{\beta}_3)\)

betahat_hu[4] - qt(0.975,15) * sqrt(hat_var_hu_b3)

-10.1858224609978

betahat_hu[4] + qt(0.975,15) * sqrt(hat_var_hu_b3)

7.43415535408522

\((x^\top x)^{-1}_{(5,5)}\)

solve(t(x_hu)%*%x_hu)[5,5]

0.790802610709727

\(MSE \sim \sigma^2\)

sum((x_hu%*%betahat_hu - df$y)**2)/15

10.3286302350608

\(var(\beta_4) = (x^\top x)^{-1}_{(5,5)} \sigma^2\)

hat_var_hu_b4 <- (solve(t(x_hu)%*%x_hu)[5,5]%*% sum((x_hu%*%betahat_hu - df$y)**2)/15)[,]
hat_var_hu_b4

8.16790775494154

sqrt(hat_var_hu_b4)

2.85795517021201

\(\beta_4 \pm t_{0.975}(15) se(\hat{\beta}_4)\)

betahat_hu[5] - qt(0.975,15) * sqrt(hat_var_hu_b4)

-8.49523514036072

betahat_hu[5] + qt(0.975,15) * sqrt(hat_var_hu_b4)

3.68793935719647

---

R code

summary(lm(df$y~x_hu))$coefficients

A matrix: 5 × 4 of type dbl

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	36.5226684	5.33137589	6.8505146	5.501546e-06
x_hu2	-0.1101234	0.01996581	-5.5155977	5.929593e-05
x_hu3	7.8990531	1.50446748	5.2503980	9.786601e-05
x_hu4	-1.3758336	4.13333214	-0.3328631	7.438444e-01
x_hu5	-2.4036479	2.85795517	-0.8410376	4.135338e-01

anova(lm(df$y~x_hu))

A anova: 2 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x_hu	4	1488.0205	372.00514	36.01689	1.586767e-07
Residuals	15	154.9295	10.32863	NA	NA

confint(lm(df$y~x_hu), level=0.95)

A matrix: 6 × 2 of type dbl

	2.5 %	97.5 %
(Intercept)	25.1591097	47.88622717
x_hu1	NA	NA
x_hu2	-0.1526795	-0.06756725
x_hu3	4.6923566	11.10574964
x_hu4	-10.1858225	7.43415535
x_hu5	-8.4952351	3.68793936

(6)

만약 적성검사점수와 성별, 적성검사점수와 학력, 성별과 학력간에 교호작용이 있다면, 다음의 반응함수를 가정할 수 있다. \[E(y)=\beta_0 +\beta_1x_1 +\beta_2x_2 +\beta_3x_3 +\beta_4x_4\] \[+ \beta_5x_1x_2 + \beta_6x_1x_3 + \beta_7x_1x_4 + \beta_8x_2x_3 + \beta_9x_2x_4\] 데이터로부터 위의 반응함수를 적합하고, 다섯 개의 다음 가설을 유의수준 \(\alpha = 0.1\)에서 검정하시오. \(H_0 :\beta_i =0, H_1 :\beta_i \neq 0(i=5,6,7,8,9)\)

answer

x_6 <- matrix(c(rep(c(1),20),df$x1,df$sex,df$high,df$univ,
                df$x1*df$sex, df$x1*df$high, df$x1*df$univ, df$sex*df$high, df$sex*df$univ),nrow=20,ncol=10)

x_6

A matrix: 20 × 10 of type dbl

1	151	0	0	1	0	0	151	0	0
1	92	0	1	0	0	92	0	0	0
1	175	0	0	1	0	0	175	0	0
1	31	0	1	0	0	31	0	0	0
1	104	0	1	0	0	104	0	0	0
1	277	0	0	0	0	0	0	0	0
1	210	0	0	0	0	0	0	0	0
1	120	0	0	1	0	0	120	0	0
1	290	0	0	0	0	0	0	0	0
1	238	0	0	0	0	0	0	0	0
1	164	1	0	0	164	0	0	0	0
1	272	1	0	0	272	0	0	0	0
1	295	1	0	0	295	0	0	0	0
1	68	1	1	0	68	68	0	1	0
1	85	1	0	1	85	0	85	0	1
1	224	1	0	0	224	0	0	0	0
1	166	1	0	1	166	0	166	0	1
1	305	1	0	0	305	0	0	0	0
1	124	1	0	1	124	0	124	0	1
1	246	1	0	0	246	0	0	0	0

betahat_6 <- solve(t(x_6)%*%x_6)%*%t(x_6)%*%df$y
betahat_6

A matrix: 10 × 1 of type dbl

36.63696518
-0.11186981
12.27994350
-3.42748073
-6.74634061
-0.01528919
0.01659028
0.03861449
0.02924469
-4.10250464

\(\hat{E}(y) = 36.63696518 - 0.11186981x_1 + 12.27994350x_2 - 3.42748073x_3 - 6.74634061x_4 - 0.01528919x_1 x_2 + 0.01659028x_1 x_3 + 0.03861449 x_1 x_4 + 0.02924469x_2 x_3 - 4.10250464x_2 x_4\)

t(x_6)%*%x_6

A matrix: 10 × 10 of type dbl

20	3637	10	4	6	1949	295	821	1	3
3637	796043	1949	295	821	446403	24865	117983	68	375
10	1949	10	1	3	1949	68	375	1	3
4	295	1	4	0	68	295	0	1	0
6	821	3	0	6	375	0	821	0	3
1949	446403	1949	68	375	446403	4624	50157	68	375
295	24865	68	295	0	4624	24865	0	68	0
821	117983	375	0	821	50157	0	117983	0	375
1	68	1	1	0	68	68	0	1	0
3	375	3	0	3	375	0	375	0	3

solve(t(x_6)%*%x_6)

A matrix: 10 × 10 of type dbl

13.17371289	-5.093089e-02	-12.267241674	-13.17371289	-8.36632222	4.731945e-02	5.093089e-02	1.859418e-02	9.049519133	5.587008431
-0.05093089	2.007129e-04	0.047358588	0.05093089	0.03198551	-1.864806e-04	-2.007129e-04	-7.327756e-05	-0.034677908	-0.021032546
-12.26724167	4.735859e-02	15.889907134	12.26724167	6.05702973	-6.112751e-02	-4.735859e-02	-5.585862e-03	-11.733236632	-7.260347528
-13.17371289	5.093089e-02	12.267241674	15.37525737	8.36632222	-4.731945e-02	-7.562090e-02	-1.859418e-02	-9.572142583	-5.587008431
-8.36632222	3.198551e-02	6.057029727	8.36632222	10.98679372	-2.278514e-02	-3.198551e-02	-4.736984e-02	-4.507640358	-3.906316822
0.04731945	-1.864806e-04	-0.061127507	-0.04731945	-0.02278514	2.414928e-04	1.864806e-04	2.145159e-05	0.044705999	0.027035225
0.05093089	-2.007129e-04	-0.047358588	-0.07562090	-0.03198551	1.864806e-04	5.270126e-04	7.327756e-05	0.037179539	0.021032546
0.01859418	-7.327756e-05	-0.005585862	-0.01859418	-0.04736984	2.145159e-05	7.327756e-05	2.668358e-04	0.004127154	0.007485293
9.04951913	-3.467791e-02	-11.733236632	-9.57214258	-4.50764036	4.470600e-02	3.717954e-02	4.127154e-03	10.045741217	5.421952259
5.58700843	-2.103255e-02	-7.260347528	-5.58700843	-3.90631682	2.703522e-02	2.103255e-02	7.485293e-03	5.421952259	4.226992806

\(MSE \sim \sigma^2\)

sum((x_6%*%betahat_6 - df$y)**2)

128.60490936452

sum((x_6%*%betahat_6 - df$y)**2)/10

12.860490936452

\(H_0: \beta_1 = 0 \text{ vs } H_1: \beta_i \neq 0 (i=5,6,7,8,9)\)

\(t_0 = \frac{\hat{\beta}_i}{\hat{s.e.}(\hat{\beta}_i)}\sim H_0 , t(n-p-1)\)

---

\(H_0 :\beta_5 =0\)

\(H_1 :\beta_5 \neq 0\)

\((x^\top x)^{-1}_{(6,6)}\)

solve(t(x_6)%*%x_6)[6,6]

0.000241492771933959

\(var(\hat{\beta}_5) = (x^\top x)^{-1}_{(6,6)} \sigma^2\)

hat_var_6_b5 <- (solve(t(x_6)%*%x_6)[6,6]*sum((x_6%*%betahat_6 - df$y)**2)/10)
hat_var_6_b5

0.00310571560467536

sqrt(hat_var_6_b5)

0.0557289476365323

\(t_0 = \frac{\beta_5}{\sqrt{\hat{var}(\hat{\beta}_5)}}\)

betahat_6[6]/sqrt(hat_var_6_b5)

-0.274349074823289

qt(0.95,10)

1.81246112281168

\(|t_0|<1.812\)가 되어 귀무가설 \(H_0 :\beta_5 =0\)은 기각할 수 없다.

---

\(H_0 :\beta_6 =0\)

\(H_1 :\beta_6 \neq 0\)

\((x^\top x)^{-1}_{(7,7)}\)

solve(t(x_6)%*%x_6)[7,7]

0.000527012620706128

\(var(\beta_6) = (x^\top x)^{-1}_{(7,7)} \sigma^2\)

hat_var_6_b6 <- (solve(t(x_6)%*%x_6)[7,7]*sum((x_6%*%betahat_6 - df$y)**2)/10)
hat_var_6_b6

0.006777641031987

\(t_0 = \frac{\beta_6}{\sqrt{\hat{var}(\hat{\beta}_6)}}\)

betahat_6[7]/sqrt(hat_var_6_b6)

0.20151831465707

qt(0.95,10)

1.81246112281168

\(|t_0|<1.812\)가 되어 귀무가설 \(H_0 :\beta_6 =0\)은 기각할 수 없다.

---

\(H_0 :\beta_7 =0\)

\(H_1 :\beta_7 \neq 0\)

\((x^\top x)^{-1}_{(8,8)}\)

solve(t(x_6)%*%x_6)[8,8]

0.000266835833441736

\(var(\beta_7) = (x^\top x)^{-1}_{(8,8)} \sigma^2\)

hat_var_6_b7 <- (solve(t(x_6)%*%x_6)[8,8]*sum((x_6%*%betahat_6 - df$y)**2)/10)
hat_var_6_b7

0.00343163981749807

\(t_0 = \frac{\beta_7}{\sqrt{\hat{var}(\hat{\beta}_7)}}\)

betahat_6[8]

0.0386144912979298

betahat_6[8]/sqrt(hat_var_6_b7)

0.659173088855045

qt(0.95,10)

1.81246112281168

\(|t_0|<1.812\)가 되어 귀무가설 \(H_0 :\beta_7 =0\)은 기각할 수 없다.

---

\(H_0 :\beta_8 =0\)

\(H_1 :\beta_8 \neq 0\)

\((x^\top x)^{-1}_{(9,9)}\)

solve(t(x_6)%*%x_6)[9,9]

10.0457412166377

\(var(\beta_8) = (x^\top x)^{-1}_{(9,9)} \sigma^2\)

hat_var_6_b8 <- (solve(t(x_6)%*%x_6)[9,9]*sum((x_6%*%betahat_6 - df$y)**2)/10)
hat_var_6_b8

129.193163866512

\(t_0 = \frac{\beta_8}{\sqrt{\hat{var}(\hat{\beta}_8)}}\)

betahat_6[9]/sqrt(hat_var_6_b8)

0.00257292605071365

qt(0.95,10)

1.81246112281168

\(|t_0|<1.812\)가 되어 귀무가설 \(H_0 :\beta_8 =0\)은 기각할 수 없다.

---

\(H_0 :\beta_9 =0\)

\(H_1 :\beta_9 \neq 0\)

\(t_0 = \frac{\beta_9}{\sqrt{\hat{var}(\hat{\beta}_9)}}\)

\((x^\top x)^{-1}_{(10,10)}\)

solve(t(x_6)%*%x_6)[10,10]

4.22699280590833

\(var(\beta_{10}) = (x^\top x)^{-1}_{(10,10)} \sigma^2\)

hat_var_6_b9 <- (solve(t(x_6)%*%x_6)[10,10]*sum((x_6%*%betahat_6 - df$y)**2)/10)
hat_var_6_b9

54.3612026688321

betahat_6[10]/sqrt(hat_var_6_b9)

-0.55642233331273

qt(0.95,10)

1.81246112281168

\(|t_0|<1.812\)가 되어 귀무가설 \(H_0 :\beta_9 =0\)은 기각할 수 없다.

---

R code

summary(lm(y ~ x1 + sex + high + univ + x1*sex + x1*high + x1*univ + sex*high + sex*univ,df))

Call:
lm(formula = y ~ x1 + sex + high + univ + x1 * sex + x1 * high + 
    x1 * univ + sex * high + sex * univ, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.6490 -1.4326 -0.1288  0.8918  5.9881 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 36.63697   13.01616   2.815   0.0183 *
x1          -0.11187    0.05081  -2.202   0.0523 .
sex         12.27994   14.29517   0.859   0.4104  
high        -3.42748   14.06177  -0.244   0.8124  
univ        -6.74634   11.88678  -0.568   0.5829  
x1:sex      -0.01529    0.05573  -0.274   0.7894  
x1:high      0.01659    0.08233   0.202   0.8443  
x1:univ      0.03861    0.05858   0.659   0.5247  
sex:high     0.02924   11.36632   0.003   0.9980  
sex:univ    -4.10250    7.37300  -0.556   0.5902  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.586 on 10 degrees of freedom
Multiple R-squared:  0.9217,    Adjusted R-squared:  0.8513 
F-statistic: 13.08 on 9 and 10 DF,  p-value: 0.0001985

anova(lm(y ~ x1 + sex + high + univ + x1*sex + x1*high + x1*univ + sex*high + sex*univ,df))

A anova: 10 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x1	1	1170.3587315	1170.3587315	91.00420328	2.444210e-06
sex	1	306.7768085	306.7768085	23.85420666	6.380709e-04
high	1	3.5791086	3.5791086	0.27830264	6.093205e-01
univ	1	7.3058980	7.3058980	0.56808857	4.683946e-01
x1:sex	1	0.6267948	0.6267948	0.04873802	8.297162e-01
x1:high	1	0.1408619	0.1408619	0.01095307	9.187174e-01
x1:univ	1	12.5166525	12.5166525	0.97326398	3.471356e-01
sex:high	1	9.0585522	9.0585522	0.70437063	4.209294e-01
sex:univ	1	3.9816828	3.9816828	0.30960581	5.901555e-01
Residuals	10	128.6049094	12.8604909	NA	NA

(7)

위의 반응함수에 대하여 회귀분석을 통한 분산분석표를 작성하고, 회귀변동의 유의성을 \(F\)-검정하시오. 이때 \(F\) -검정의 귀무가설을 \(\beta_i\) 들로 표현하시오.

answer

\(SST\)

SST <- sum((df$y - (17+26+21+30+22+1+12+19+4+16+28+15+11+38+31+21+20+13+30+14)/20)**2)
SST

1642.95

\(SSR\)

SSR_7 <- sum(((17+26+21+30+22+1+12+19+4+16+28+15+11+38+31+21+20+13+30+14)/20 - x_6%*%betahat_6)**2)
SSR_7

1514.34509063554

\(MSR\)

MSR_7 <- SSR_7/9
MSR_7

168.260565626172

\(SSE\)

SSE_7 <- SST - SSR_7
SSE_7

128.604909364456

\(MSE\)

MSE_7 <- SSE_7/10
MSE_7

12.8604909364456

\(F_0\)

F0_7 <- MSR_7 / MSE_7
F0_7

13.0835258512048

qf(0.95,9,10)

3.02038294702137

	제곱합	자유도	평균제곱합	F_0	F_{0.05}(9,10)
회귀	1514.35	9	168.26	13.084	3.0204
잔차	128.6	10	12.86
합계	1642.95	19

\(H_0 : \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = \beta_6 = \beta_7 = \beta_8 = \beta_9 = 0\)

\(H_1 : \text{not } H_0\)

\(|F_0|>3.0204\)가 되어 귀무가설 \(H_0 : \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = \beta_6 = \beta_7 = \beta_8 = \beta_9 = 0\)은 기각한다.

따라서 유의수준 0.05에서 회귀모형이 유의함을 알 수 있다.

---

R code

round(anova(lm(y ~ x1 + sex + high + univ + x1*sex + x1*high + x1*univ + sex*high + sex*univ,df)),4)

A anova: 10 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
x1	1	1170.3587	1170.3587	91.0042	0.0000
sex	1	306.7768	306.7768	23.8542	0.0006
high	1	3.5791	3.5791	0.2783	0.6093
univ	1	7.3059	7.3059	0.5681	0.4684
x1:sex	1	0.6268	0.6268	0.0487	0.8297
x1:high	1	0.1409	0.1409	0.0110	0.9187
x1:univ	1	12.5167	12.5167	0.9733	0.3471
sex:high	1	9.0586	9.0586	0.7044	0.4209
sex:univ	1	3.9817	3.9817	0.3096	0.5902
Residuals	10	128.6049	12.8605	NA	NA

2.

아래의 데이터에 대하여 다음 물음에 답하시오.

\(x\)	1	2	2	3	4	5	5	6	7
\(y\)	2.0	3.2	3.2	4.1	5.2	7.0	7.4	9.7	11.5

df2 <- data.frame('y'=c(2.0,3.2,3.2,4.1,5.2,7.0,7.4,9.7,11.5),'x1'=c(1,2,2,3,4,5,5,6,7))

(1)

\(x\)와 \(y\)에 대한 산점도를 그려보고, 어떤 \(x\)의 값(\(x_w\))에서 구간을 두 개로 나누면 적절한지 논하시오.

answer

plot(df2$x1,df2$y)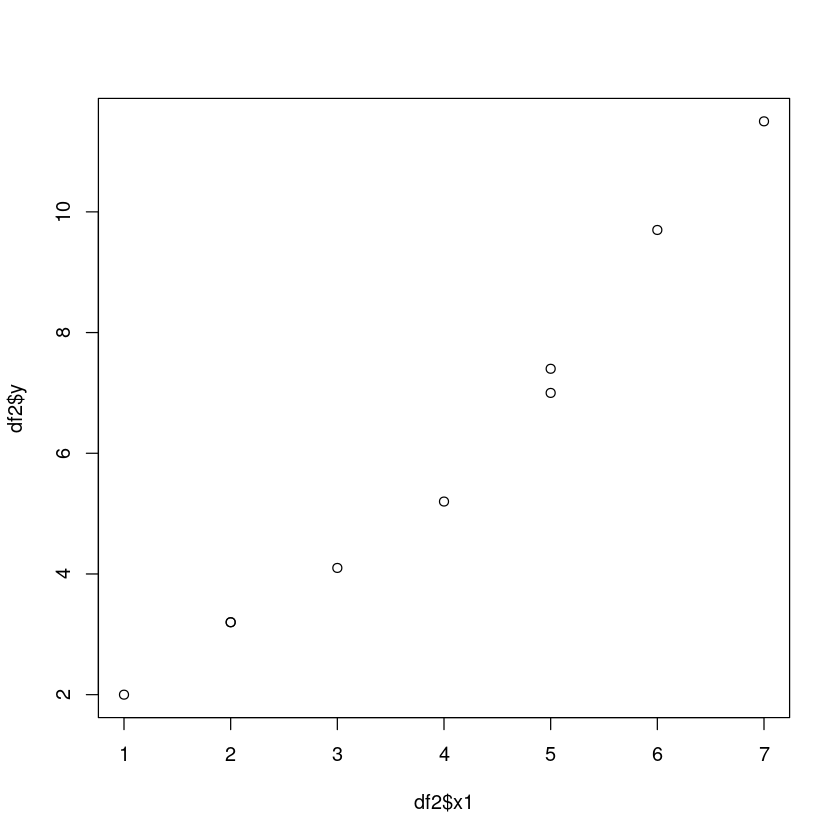

산점도를 그려보면 \(x = 4\)를 기준으로 기울기가 달라지는 것으로 보인다.

(2)

위의 (1)에서 얻은 점을 경계로 구간별 단순선형회귀선을 추정하시오. 사용되는 모형은 \[x_{2i} = \begin{cases} 1 :& \text{만약 }x_{1i} > x_w \text{ 이면 }\\ 0 : &\text{만약 } x_{1i} \le x_w \text{ 이면 } \end{cases}\] 과 같다.

answer

plot(df2$x1,df2$y)
abline(v=4,col="red",lty=2)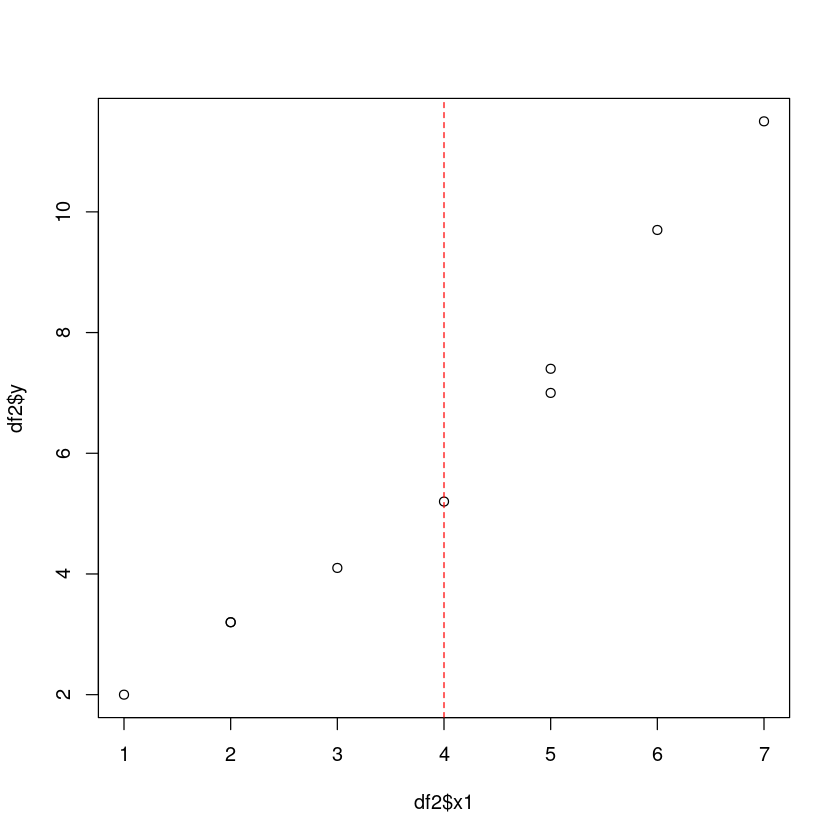

df2$x2 <- sapply(df2$x1, function(x) max(0, x-4))

x_sp <- matrix(c(rep(1,9),df2$x1,df2$x2),nrow=9,ncol=3)

x_sp

A matrix: 9 × 3 of type dbl

1	1	0
1	2	0
1	2	0
1	3	0
1	4	0
1	5	1
1	5	1
1	6	2
1	7	3

betahat_sp <- solve(t(x_sp)%*%x_sp)%*%t(x_sp)%*%df2$y
betahat_sp

A matrix: 3 × 1 of type dbl

1.071429

1.023469

1.119388

---

R code

model_1 <- lm(y ~ x1+x2, df2)

summary(model_1)

Call:
lm(formula = y ~ x1 + x2, data = df2)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.30816 -0.09388  0.03469  0.08163  0.24898 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.07143    0.19695   5.440 0.001602 ** 
x1           1.02347    0.06973  14.677 6.28e-06 ***
x2           1.11939    0.12937   8.652 0.000131 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1823 on 6 degrees of freedom
Multiple R-squared:  0.9976,    Adjusted R-squared:  0.9968 
F-statistic:  1242 on 2 and 6 DF,  p-value: 1.4e-08

df2_2 <- rbind(df2[,2:3], c(4,0))

df2_2$y <- predict(model_1, newdata = df2_2)

this is the predicted line of multiple linear regression

ggplot(data = df2, aes(x = x1, y = y)) + 
  geom_point(color='steelblue') +
  geom_line(color='darkorange',data = df2_2, aes(x=x1, y=y))+
  geom_vline(xintercept = 4, lty=2, col='red')+
  theme_bw()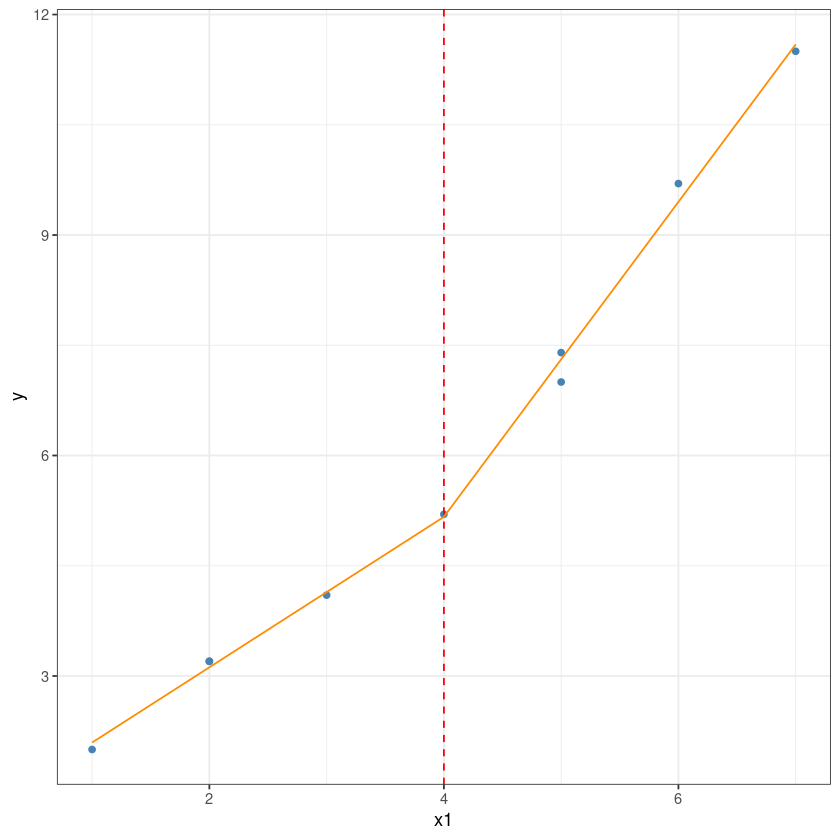

(3)

위의 (2)에 있는 모형에서 \(\beta_2\) 의 90% 신뢰구간을 구하고, 그 의미를 해석하시오.

answer

t(x_sp)%*%x_sp

A matrix: 3 × 3 of type dbl

9	35	7
35	169	43
7	43	15

solve(t(x_sp)%*%x_sp)

A matrix: 3 × 3 of type dbl

1.1666667	-0.3809524	0.5476190
-0.3809524	0.1462585	-0.2414966
0.5476190	-0.2414966	0.5034014

\((x^\top x)^{-1}_{(3,3)}\)

solve(t(x_sp)%*%x_sp)[3,3]

0.503401360544218

\(MSE \sim \sigma^2\)

SSE_sp <- sum((df2$y - x_sp%*%betahat_sp)**2)
SSE_sp

0.199489795918367

MSE_sp <- SSE_sp/(9-2-1)
MSE_sp

0.0332482993197279

\(var(\beta_2) = (x^\top x)^{-1}_{(3,3)} \sigma^2\)

hat_var_b2_sp <- solve(t(x_sp)%*%x_sp)[3,3] * MSE_sp
hat_var_b2_sp

0.0167372391133324

sqrt(hat_var_b2_sp)

0.129372482056009

\(\beta_2 \pm t_{0.95}(6) se(\hat{\beta}_2)\)

betahat_sp[3] - qt(0.95,6) * sqrt(hat_var_b2_sp)

0.867993699129489

betahat_sp[3] + qt(0.95,6) * sqrt(hat_var_b2_sp)

1.3707818110746

\(\beta_2\)는 기울기의 차이이다.

90% 시뢰구긴이 0을 포함하지 않고 모두 양수이므로, \(\beta_2 \neq 0\)이라고 90% 확신할 수 있다.

즉 구간별 회귀직선의 기울기는 다르다고 할 수 있다.(유의수준 0.1)

---

R code

summary(model_1)

Call:
lm(formula = y ~ x1 + x2, data = df2)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.30816 -0.09388  0.03469  0.08163  0.24898 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.07143    0.19695   5.440 0.001602 ** 
x1           1.02347    0.06973  14.677 6.28e-06 ***
x2           1.11939    0.12937   8.652 0.000131 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1823 on 6 degrees of freedom
Multiple R-squared:  0.9976,    Adjusted R-squared:  0.9968 
F-statistic:  1242 on 2 and 6 DF,  p-value: 1.4e-08

anova(model_1)

A anova: 3 × 5

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x1	1	80.0869407	80.0869407	2408.75300	4.798337e-09
x2	1	2.4891251	2.4891251	74.86473	1.313702e-04
Residuals	6	0.1994898	0.0332483	NA	NA

confint(model_1, level=0.90)

A matrix: 3 × 2 of type dbl

	5 %	95 %
(Intercept)	0.6887173	1.454140
x1	0.8879634	1.158975
x2	0.8679937	1.370782