고급회귀분석 과제, CH03, CH04

과제1

풀이 :

R 이용하지 않고 직접 계산. (R로 단순 계산은 해도 됨)

모든 문제에는 풀이가 있어야 함.

풀이 없이 답만 있는 경우 ’0’점 처리.

제출 기한 : 10월 03일

제출 방법 :

직접 제출 (607호) 또는 스캔, 사진, tex 작업, 문서 작업 등 후 pdf로 변환 후 제출

pdf 아닌 경우 미제출 처리

1.

원점을 지나는 회귀모형은 다음과 같이 정의할 수 있다. \[y_i =β_1x_i +ε_i, ε_i ∼_{i.i.d.} N(0,σ^2), i=1,...,n\] 오차제곱합을 정의하고 \(β_1\) 의 최소제곱추정량 (\(\hat{β}_1\))을 구하여라.

Answer

\(SSE = \sum(y_i - \hat{y_i})^2 = \sum(y_i - \hat{\beta_1}x_i)^2\)

\(SSE' = 0 = \sum(-x_i)2(y_i - \hat{\beta_1}x_i )\)

\(\sum(-x_iy_i) + \sum(x_i^2\hat{\beta_1}) = 0\)

\(\hat{\beta_1} = \frac{\sum(x_iy_i)}{\sum(x_i^2)}\)

2.

자동차의 무게가 무거우면 이를 움직이는 데 더 많은 연료가 소모된다는 것은 알려진 사실이다. 자동차의 무게와 자동차를 1km 움직이는 데 필요한 에너지량과의 함수관계를 정확히 판단하기 위하여 A 자동차회사는 다음의 자료를 실험을 통하여 얻었다. 실험 비용이 많이 드는 관계로 9번만 실험하였다.

무게 X(단위: 1,000kg)	에너지소모량 Y(단위: 1,000btu)
0.9	2.0
1.3	2.6
2.1	4.3
2.5	5.8
2.4	5.1
1.7	3.2
0.7	1.8
1.2	2.3
1.6	3.0

(1)

이 데이터의 산점도를 그리시오.

dt <- data.frame(x = c(0.9,1.3,2.1,2.5,2.4,1.7,0.7,1.2,1.6),
                 y = c(2.0,2.6,4.3,5.8,5.1,3.2,1.8,2.3,3.0))
dt

A data.frame: 9 × 2
x	y
<dbl>	<dbl>
0.9	2.0
1.3	2.6
2.1	4.3
2.5	5.8
2.4	5.1
1.7	3.2
0.7	1.8
1.2	2.3
1.6	3.0

Answer

plot(y~x, 
     data = dt,
     xlab = "무게",
     ylab = "에너지소모량",
     pch  = 16,
     cex  = 1,
     col  = "darkorange")

양의 상관관계가 있어보인다.
무게가 커질수록 에너지소모량도 큰 경향이 보이기 때문이다.
우상향의 모양이라, 단순상관선형 적용해보면 되겠다.

(2)

최소제곱법의 의한 회귀직선을 적합시키시오.

Answer

dt1 <- data.frame(
  i = 1:nrow(dt),
  x = dt$x,
  y = dt$y,
  x_barx = dt$x - mean(dt$x),
  y_bary = dt$y - mean(dt$y))

\(S_{xx}, S_{yy},S_{xy}\)를 구해주기 위해 \(x_i - \bar{x}, y_i - \bar{y}\)를 구했다.

dt1$x_barx2 <- dt1$x_barx^2
dt1$y_bary2 <- dt1$y_bary^2
dt1$xy <-dt1$x_barx * dt1$y_bary

\(S_{xx}, S_{yy},S_{xy}\)를 구해주었다.

dt1

A data.frame: 9 × 8
i	x	y	x_barx	y_bary	x_barx2	y_bary2	xy
<int>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	0.9	2.0	-0.7	-1.3444444	0.49	1.8075309	0.94111111
2	1.3	2.6	-0.3	-0.7444444	0.09	0.5541975	0.22333333
3	2.1	4.3	0.5	0.9555556	0.25	0.9130864	0.47777778
4	2.5	5.8	0.9	2.4555556	0.81	6.0297531	2.21000000
5	2.4	5.1	0.8	1.7555556	0.64	3.0819753	1.40444444
6	1.7	3.2	0.1	-0.1444444	0.01	0.0208642	-0.01444444
7	0.7	1.8	-0.9	-1.5444444	0.81	2.3853086	1.39000000
8	1.2	2.3	-0.4	-1.0444444	0.16	1.0908642	0.41777778
9	1.6	3.0	0.0	-0.3444444	0.00	0.1186420	0.00000000

반올림 해주었다.

round(colSums(dt1),3)

i: 45
x: 14.4
y: 30.1
x_barx: 0
y_bary: 0
x_barx2: 3.26
y_bary2: 16.002
xy: 7.05

\(\hat{\beta_1} = \frac{S_{xy}}{S_{xx}}\)

\(\hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\)

beta1 <- as.numeric(colSums(dt1)[8]/colSums(dt1)[6])
beta0 <- mean(dt$y) - beta1 *  mean(dt$x)

cat("hat beta0 = ", beta0)
cat("hat beta1 = ", beta1)

hat beta0 =  -0.1156783hat beta1 =  2.162577

\(\hat{y} = -0.1156783 + 2.162577x\)의 모형으로 적합되었다.

lm(y~x,dt)


Call:
lm(formula = y ~ x, data = dt)

Coefficients:
(Intercept)            x  
    -0.1157       2.1626

(3)

데이터의 산점도를 그리고 추정한 회귀직선을 (1)에서 그린 산점도 위에 그리시오.

Answer

plot(y~x, 
     data = dt,
     xlab = "무게",
     ylab = "에너지소모량",
     pch  = 16,
     cex  = 1,
     col  = "darkorange")
par(new=TRUE)
plot(-0.1156783 +  2.162577*x~x,
     data = dt,
     xlab = "",
     ylab = "",
     pch  = 16,
     cex  = 1,type='l',
     col  = "blue")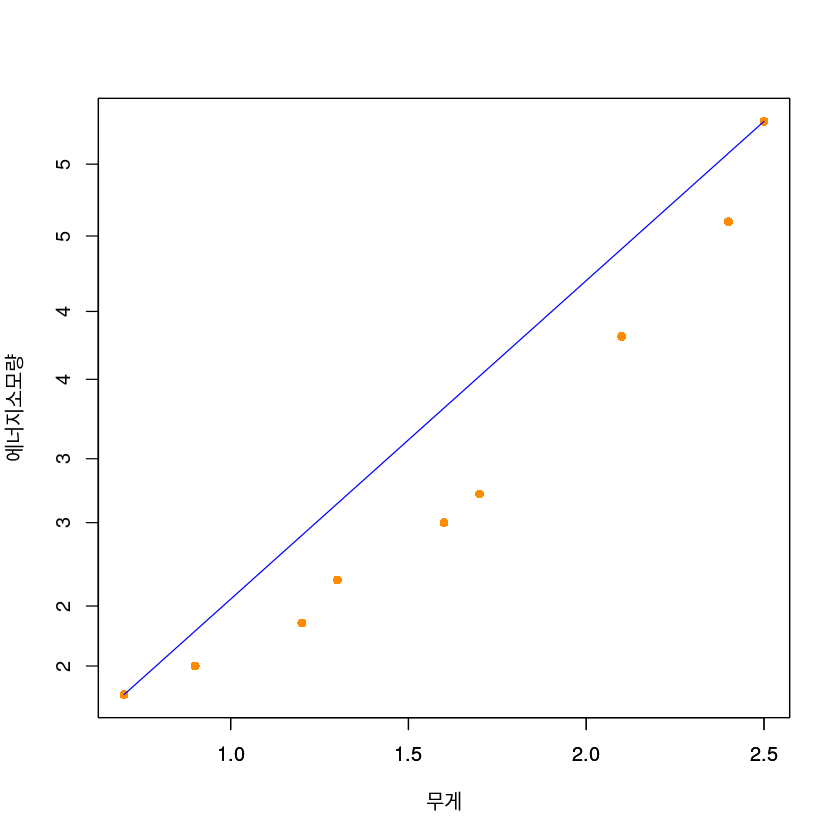

추정한 회귀직선을 그려보니 오차가 클 것처럼 y와 \(\hat{y}\)가 떨어진 값이 많아보인다.

(4)

결정계수와 상관계수를 구하시오.

\(r_{xy} = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}}\)

rxy = colSums(dt1)[8]/sqrt(colSums(dt1)[6]*colSums(dt1)[7])
rxy

xy: 0.976090685311348

상관계수는 약 98% 로, \(x,y\)간 높은 양의 상관관계가 있었다.

\(R^2 = \frac{SSR}{SST} = r^2\)

SST = sum((dt$y - mean(dt$y))^2)

SSR = sum( ( (-0.1156783 +  2.162577*dt$x)-mean(dt$y) )^2 )

SSE = sum( ( dt$y-(-0.1156783 +  2.162577*dt$x))^2 )

cat("SST = ", SST)
cat("\nSSR = ", SSR)
cat("\nSSE = ", SSE)

SST =  16.00222
SSR =  15.24617
SSE =  0.7560566

SSR/SST

0.95275330164195

rxy**2

xy: 0.952753025951577

결정계수는 약 95%로, 설명력도 높은 편이라고 말할 수 있지만, 결정계수는 다른 모델과 비교할때 언급되는 것이 적절하다.

(5)

분산분석표를 작성하고 회귀직선의 유의 여부를 검정하시오 (유의수준 \(α = 0.05\) 사용).

MSR = SSR/1
MSE = SSE/7

cat("MSR = ", MSR)
cat("\nMSE = ", MSE)

MSR =  15.24617
MSE =  0.1080081

Fvalue = MSR/MSE

cat("F value = ",Fvalue)

F value =  141.1577

cat("p value = ",df(Fvalue,1,7))

p value =  1.614709e-07

	df	sum of square	mean of square	F value	p value
x	1	15.24617	15.24617	141.1584	1.614672e-07
Residuals	7	0.7560522	0.1080075

F값은 141.1584, p value는 1.614672e-07가 나왔다.
유의수준 5%에서 모형이 유의하다는 것을 알 수 있었다.

anova(lm(y~x,dt))

A anova: 2 × 5
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x	1	15.2461656	15.2461656	141.1576	6.798033e-06
Residuals	7	0.7560566	0.1080081	NA	NA

(6)

\(\beta_0,\beta_1\) 에 대한 90% 신뢰구간을 구하시오.

Answer

\[\hat{\beta_0} \pm t_{(\alpha/2,n-2)}\hat{\sigma} \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{S_{xx}}}\]

cat("Beta0 confidence level",beta0 + qt(0.025, 7) * sqrt((MSE)*(1/9 + mean(dt$x)^2/sum((dt$x - mean(dt$x))^2))),"~",beta0 + qt(0.975, 7) * sqrt((MSE)*(1/9 + mean(dt$x)^2/sum((dt$x - mean(dt$x))^2))))

Beta0 confidence level -0.8514415 ~ 0.620085

\[\hat{\beta_1} \pm t_{(\alpha/2,n-2)} \sqrt{\frac{MSE}{S_{xx}}}\]

cat("Beta1 confidence level",beta1 + qt(0.025, 7) * sqrt((MSE)/sum((dt$x - mean(dt$x))^2)),'~',beta1 + qt(0.975, 7) * sqrt((MSE)/sum((dt$x - mean(dt$x))^2)))

Beta1 confidence level 1.732168 ~ 2.592986

\(\beta_0\)의 신뢰구간은 0을 포함하였다.(\(H_0 : \beta_0=0\) 채택)
\(\beta_1\)의 신뢰구간은 0을 포함하지 않았다.(\(H_0 : \beta_1=0\) 기각)
신뢰구간으로 신뢰구간에 0이 포함된 \(\beta_1\) 계수만 유의미하다는 것을 알 수 있다.

(7)

\(H_0 :\beta_1 =1\) vs. \(H_1 :\beta_1 \ne 1\)의 가설검정을 유의수준 \(α=0.1\)에서 수행하시오.

\[\text{t value} = \frac{\hat{\beta_1} - 1}{s.e(\hat{\beta_1})}\]

Tvalue = (beta1 - 1)/(sqrt((MSE/sum((dt$x - mean(dt$x))^2))))

Tvalue

6.3870789106442

-Tvalue

-6.3870789106442

qt(0.95,7)

1.89457860509001

qt(0.05,7)

-1.89457860509001

구힌 t value = 6.39가 유의수준 \(\alpha = 0.1\) 에서의 t value = 1.89보다 크기 때문에 유의하다는 결과가 나와 귀무가설을 기각한다.
따라서 \(\beta_1\)은 1이 아니다.

figure로 표현

par(mfrow=c(1,1))
basic <- seq(-3,3,by=0.01)
plot(basic,dt(basic,df=7),type="l",xlim=c(-8,8))
abline(v=Tvalue,col="red",lty=2)
abline(v=qt(0.95,7),col="blue",lty=2)
text(x=Tvalue, y=c(0.2), labels=c("tvalue\n6.39"), pos=4, col="black")
text(x=qt(0.95,7), y=c(0.2), labels=c("t(0.05,7)\n1.89"), pos=4, col="black")
abline(v=-Tvalue,col="red",lty=2)
abline(v=qt(0.05,7),col="blue",lty=2)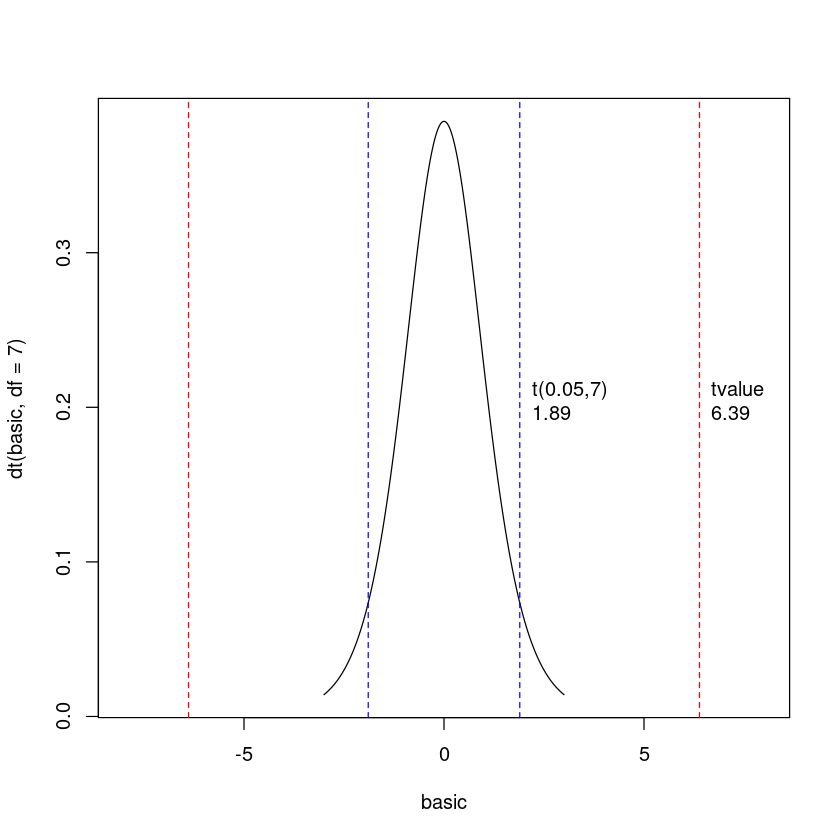

(8)

무게가 3,000kg 이 되는 차량의 평균 에너지 소모량을 예측하시오. 이것은 무게가 1,000kg이 되는 차량의 에너지 소모량의 몇 배인가?

\[\hat{\mu}_0 = \hat{\beta_0} + \hat{\beta_1} x_0\]

cat("평균 에너지 소모량 = ",beta0 + beta1 * 3)

평균 에너지 소모량 =  6.372052

cat("무게가 3,000kg 이 되는 차량의 평균 에너지 소모량을 예측해보니 무게가 1,000kg이 되는 차량의 에너지 소모량의",(beta0 + beta1 * 3)/(beta0 + beta1 * 1),"배 였다.")

무게가 3,000kg 이 되는 차량의 평균 에너지 소모량을 예측해보니 무게가 1,000kg이 되는 차량의 에너지 소모량의 3.113028 배 였다.

(9)

무게가 3,000kg 이 되는 차량의 평균 에너지 소모량과 하나의 개별 \(y\) 값의 90% 신뢰구간을 각각 구하시오.

Answer

cat("무게가 3,000kg 이 되는 차량의 평균 에너지 소모량은",beta0 + beta1 * 3,"이다.")

무게가 3,000kg 이 되는 차량의 평균 에너지 소모량은 6.372052 이다.

\[\hat{Var(\hat{\mu}_0}) = \sigma (\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}})\]

sigma = MSE

mean(dt$x)

1.6

\(S_{xx}\)

sum((dt$x - mean(dt$x))^2)

3.26

colSums(dt1)[6]

x_barx2: 3.26

\(\hat{Var(\hat{\mu_0})}\)

sqrt(sigma)*(1/9 + (3-1.6)^2/3.26)

0.234106948837031

cat("hat var(hat mu zero) = ",sqrt(sigma)*(1/9 + (3-1.6)^2/3.26))

hat var(hat mu zero) =  0.2341069

\(\hat{\sigma}_{\hat{\mu_0}}\)

sqrt(sqrt(sigma)*(1/9 + (3-1.6)^2/3.26))

0.483845997024912

cat("hat sigma(hat mu zero) = ", sqrt(sqrt(sigma)*(1/9 + (3-1.6)^2/3.26)))

hat sigma(hat mu zero) =  0.483846

\(\hat{\mu_0} \pm t_{(\alpha/2,(n-2))}\hat{\sigma_{\hat{\mu_0}}}\)

6.372052 + qt(0.95,7)*sqrt(sqrt(sigma)*(1/9 + (3-1.6)^2/3.26))

7.28873627412184

6.372052 - qt(0.95,7)*sqrt(sqrt(sigma)*(1/9 + (3-1.6)^2/3.26))

5.45536772587816

cat("개별 y값의 90% 신뢰구간은 (",5.4553690631157,"~",7.2887349368843,") 이다.")

개별 y값의 90% 신뢰구간은 ( 5.455369 ~ 7.288735 ) 이다.

(10)

잔차 \(e_i = y_i − \hat{y}_i\) 를 구하고 잔차의 합이 0 임을 확인하시오.

Answer

epsilon = dt$y - (beta0 + beta1*dt$x)

epsilon

0.169359236537151
-0.0956714383094752
-0.125732788002726
0.509236537150648
0.0254942058623033
-0.3607021131561
0.401874573960464
-0.179413769597819
-0.344444444444445

cat("잔차의 합 = ",sum(epsilon))

잔차의 합 =  8.881784e-16

합이 0인 것을 확인했다.

(11)

잔차들의 \(x_i\) 에 대한 가중합, \(\sum x_ie_i\) 를 구하시오.

sum(dt$x * epsilon)

9.99200722162641e-16

잔차들의 \(x_i\) 에 대한 가중합, \(\sum x_ie_i\)이 0인 것을 확인했다.

(12)

잔차들의 \(\hat{y}\)에 대한 가중합 \(\sum \hat{y}_ie_i\), 를 구하시오.

sum((beta0 + beta1*dt$x)*epsilon)

1.74860126378462e-15

잔차들의 \(\hat{y}\)에 대한 가중합 \(\sum \hat{y}_ie_i\)이 0인 것을 확인했다.

(13)

원점을 지나는 회귀직선을 구하시오.

Answer

\(\hat{\beta_1} = \frac{\sum(x_iy_i)}{\sum(x_i^2)}\)

sum(dt$x * dt$y)/sum((dt$x^2))

2.09923954372624

beta1_0 <- sum(dt$x * dt$y)/sum((dt$x^2))

cat("hat beta1_0 = ", beta1_0)

hat beta1_0 =  2.09924

원점을 지나는 회귀직선은 \(\hat{y} = 2.09924x\)의 모형으로 적합되었다.

(14)

위 회귀직선에서 회귀계수(기울기)의 90% 신뢰구간을 구하시오.

Answer

\[\hat{\beta_1} \pm t_{(\alpha/2,n-1)}\frac{\hat{\sigma}}{\sqrt{S_{xx}}}\]

colSums(dt1)[6]

x_barx2: 3.26

SSR_0 = sum( ( (2.09924*dt$x) )^2 )

SSE_0 = sum((dt$y - 2.09924*dt$x)^2)

SST_0 = sum(dt$y^2)

MSE_0 = SSE_0/8

MSR_0 = SSR_0/1

sigma_0 = sqrt(MSE_0)

beta1_0 + qt(0.95,8) * sigma_0/sqrt(3.26)

2.41896448320474

beta1_0 - qt(0.95,8) * sigma_0/sqrt(3.26)

1.77951460424773

cat("원점을 지나는 회귀직선에서 회귀계수(기울기)의 90% 신뢰구간은 (",beta1_0 - qt(0.95,8) * sigma_0/sqrt(3.26),"~",beta1_0 + qt(0.95,8) * sigma_0/sqrt(3.26),")이다.")

원점을 지나는 회귀직선에서 회귀계수(기울기)의 90% 신뢰구간은 ( 1.779515 ~ 2.418964 )이다.

\(\beta_1\)의 신뢰구간은 0을 포함하지 않았다.(\(H_0 : \beta_1=0\) 기각)
신뢰구간으로 신뢰구간에 0이 포함된 \(\beta_1\) 계수가 유의미하다는 것을 알 수 있다.

(15)

원점을 지나는 회귀직선의 결정계수를 구하시오.

Answer

\(R^2 = \frac{SSR}{SST} = r^2\)

SSR_0/SST_0

0.993392179573841

cat("원점을 지나는 회귀직선의 결정계수는 ", SSR_0/SST_0,"로 약",round(SSR_0/SST_0,2),"% 였다.")

원점을 지나는 회귀직선의 결정계수는  0.9933922 로 약 0.99 % 였다.

(16)

원점을 포함한 회귀직선과 포함하지 않은 회귀직선의 결과를 비교하여라.

Answer

cat("원점을 포함하지 않는 회귀직선의 결정계수는 ",SSR/SST,"로, 원점을 포함하는 회귀직선의 결정계수인 ",SSR_0/SST_0,"보다 작다.")

원점을 포함하지 않는 회귀직선의 결정계수는  0.9527533 로, 원점을 포함하는 회귀직선의 결정계수인  0.9933922 보다 작다.

cat("원점을 포함하지 않는 회귀직선의 평균재곱오차는 ",MSE,"이며, 원점을 포함하는 회귀직선의 평균제곱오차는 ",MSE_0,"이다. 원점을 포함하는 모형의 오차가 조금 더 작았다.")

원점을 포함하지 않는 회귀직선의 평균재곱오차는  0.1080081 이며, 원점을 포함하는 회귀직선의 평균제곱오차는  0.0963731 이다. 원점을 포함하는 모형의 오차가 조금 더 작았다.

Fvalue = MSR/MSE

Fvalue_0 = MSR_0 / MSE_0

cat("원점을 포함하지 않는 회귀직선의 F 값은 ",Fvalue,"로, 원점을 포함하는 회귀직선의 F 값인 ",Fvalue_0,"보다 작다. 따라서 원점을 포함한 모델이 회귀모형애 의해 설명되는 부분이 더 크며, 오차항에 기인된 부분이 더 작다.")

원점을 포함하지 않는 회귀직선의 F 값은  141.1577 로, 원점을 포함하는 회귀직선의 F 값인  1202.608 보다 작다. 따라서 원점을 포함한 모델이 회귀모형애 의해 설명되는 부분이 더 크며, 오차항에 기인된 부분이 더 작다.

cat("원점을 포함하지 않는 회귀직선의 p value 는 ",df(Fvalue,1,7),"로, 원점을 포함하는 회귀직선의 p value인",df(Fvalue_0,1,8),"과 같이 p value이 충분히 작아 두 모형이 모두 유의함을 알 수 있었다.")

원점을 포함하지 않는 회귀직선의 p value 는  1.614709e-07 로, 원점을 포함하는 회귀직선의 p value인 1.728622e-12 과 같이 p value이 충분히 작아 두 모형이 모두 유의함을 알 수 있었다.

plot(beta0 + beta1*x~x,
     data = dt,
     xlab = "원점을 지나지 않는 모형",
     ylab = "",
     pch  = 16,
     cex  = 1,type='l',
     col  = "blue")
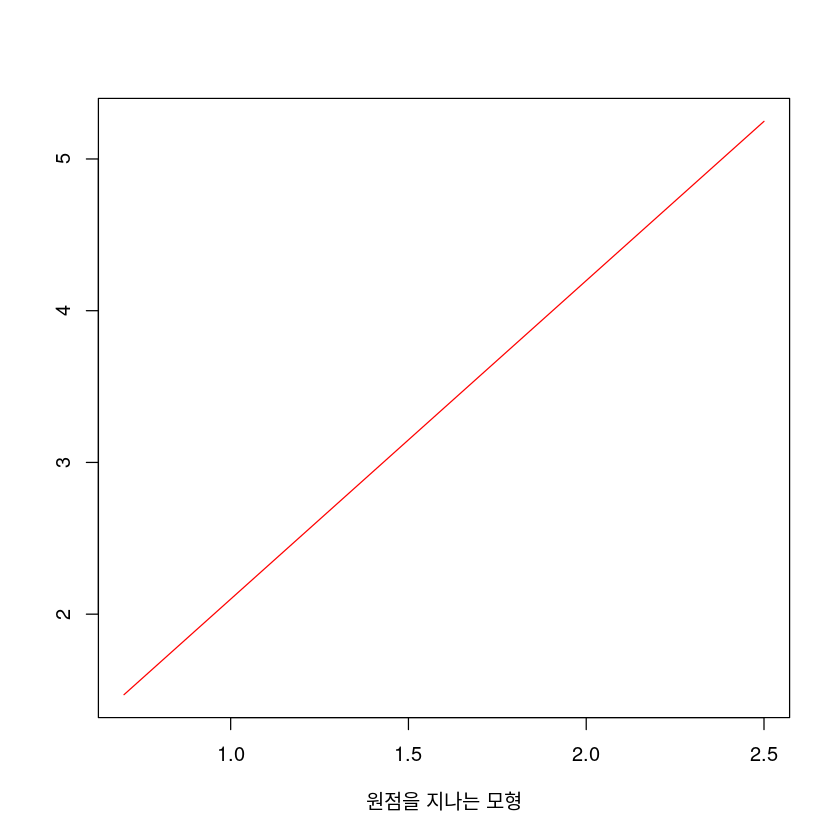
plot(beta1_0*x~x,
     data = dt,
     xlab = "원점을 지나는 모형",
     ylab = "",
     pch  = 16,
     cex  = 1,type='l',
     col  = "red")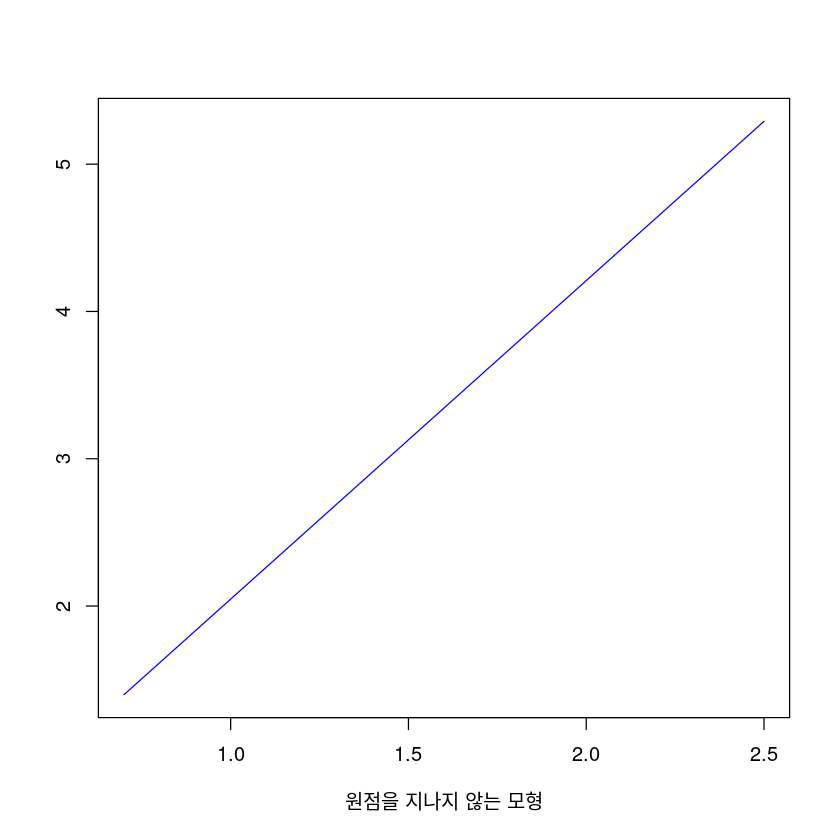

선형성 만족

epsilon = dt$y - beta0 + beta1*dt$x
epsilon_0 = dt$y - beta1_0*dt$x

plot(epsilon,
     xlab = "원점을 지나지 않는 모형",
     ylab = "",
     pch  = 16,
     cex  = 1,
     col  = "blue")
plot(epsilon_0,
     xlab = "원점을 지나는 모형",
     ylab = "",
     pch  = 16,
     cex  = 1,
     col  = "red")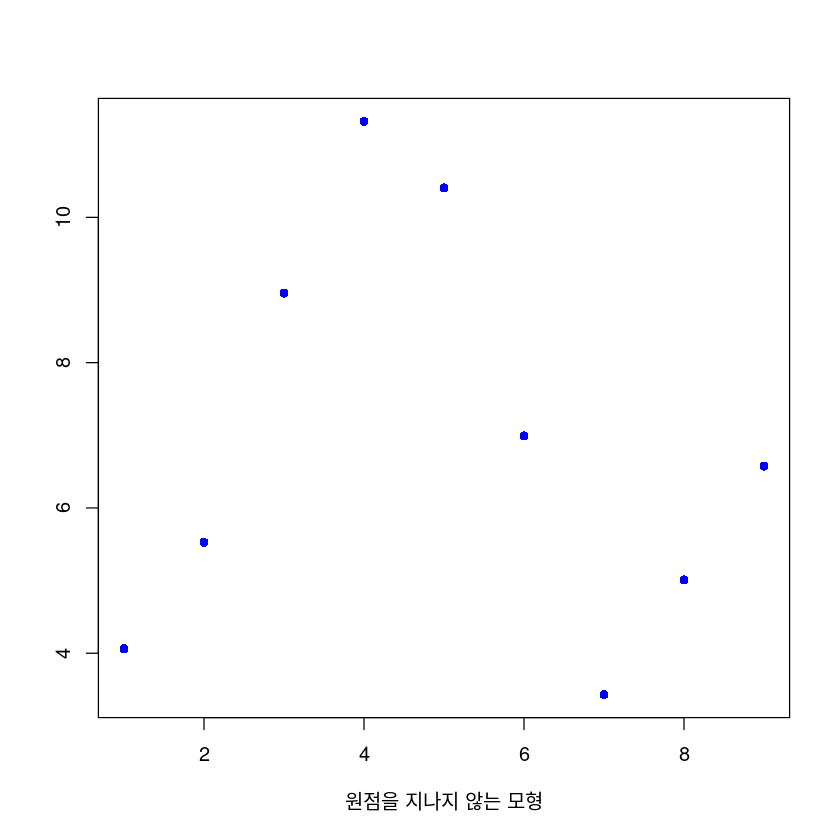

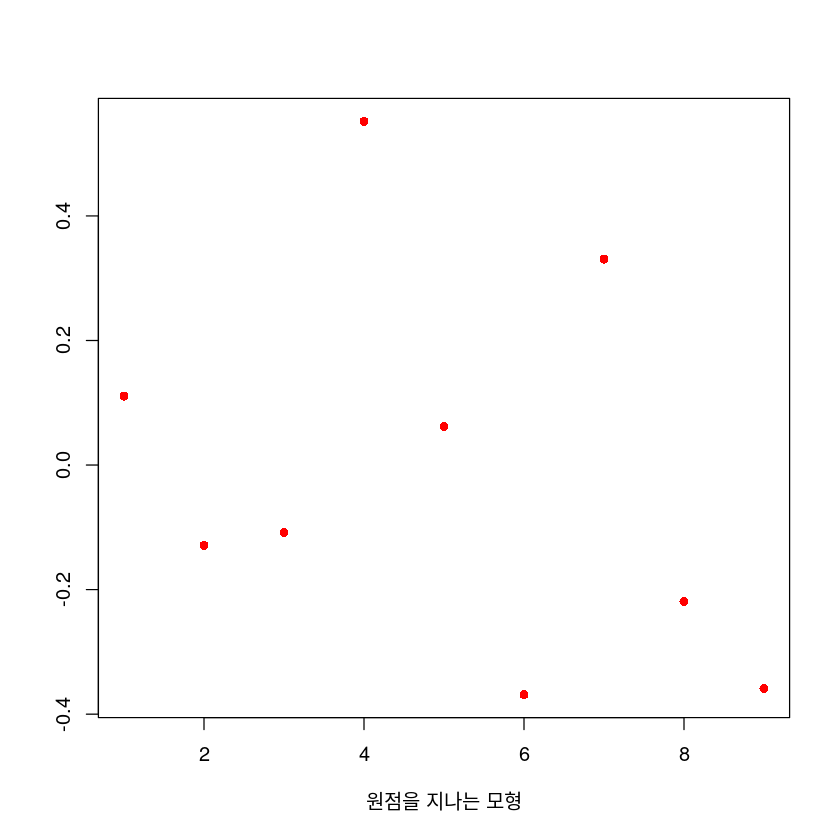
원점을 지나지 않는 모형이 한쪽 부호에 머무는 경향이 있어보인다.(독립성을 만족하지 않을 수 있다.)
원점을 지나는 모형은 그러한 경향이 없고, 등분산성을 만족하는 것처럼 보인다.

shapiro.test(beta0 + beta1*dt$x)


    Shapiro-Wilk normality test

data:  beta0 + beta1 * dt$x
W = 0.95279, p-value = 0.7207

shapiro.test(beta1_0*dt$x)


    Shapiro-Wilk normality test

data:  beta1_0 * dt$x
W = 0.95279, p-value = 0.7207

두 모형 모두 정규성 가정을 만족했다.

ANOVA table 비교

y=beta0+beta1x	df	sum of square	mean of square	F value	p value
x	1	15.24617	15.24617	141.1584	1.614672e-07
Residuals	7	0.7560522	0.1080075

y=beta1x	df	sum of square	mean of square	F value	p value
x	1	115.89906559088	115.89906559088	1202.60806139735	1.728622e-12
Residuals	8	0.77098479088	0.09637309886

3.

(강의노트 CH04, p9) 다음이 성립함을 증명하시오.

\[\hat{\beta}_0 \sim N\big( \beta_0 , \sigma^2\big( \frac{1}{n} + \frac{\bar{x}^2}{S_{(xx)}} \big) \big)\]

Answer

\(\hat{\beta_0}\)

\(= \bar{y} - \hat{\beta_1} \bar{x} = \bar{y} - \frac{S_{xy}}{S_{xx}}\bar{x}\)

\(= \bar{y} - \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{S_{xx}}\bar{x}\)

\(= \bar{y} - \sum\frac{(x_i-\bar{x})y_i\bar{x}-(x_i - \bar{x})\bar{y}\bar{x}}{S_{xx}}\)

\(= \bar{y} - \sum\frac{(x_i - \bar{x})}{S_{xx}}y_i\bar{x} - \frac{\bar{x}\bar{y}}{S_{xx}}\sum(x_i - \bar{x})\)

\(= \bar{y} - \sum\frac{(s_i - \bar{x})}{S_{xx}}y_i\bar{x}\)

\(\approx \bar{y} - \sum a_iy_i\bar{x}\)

\(E(\hat{\beta_0})\)

\(=\bar{y} - \bar{x}\sum a_i E(y_i)\)

\(=\bar{y} - \bar{x}\sum a_i (\beta_0 + \beta_1 x_i)\)

\(=\bar{y} - (\beta_0\bar{x}\sum a_i + \beta_1 \bar{x} \sum a_i x_i)\)

\(=\bar{y} - \beta_1\bar{x} = \beta_0\)

\(\star \sum a_i = \sum\frac{x_i - \bar{x}}{S_{xx}} = \frac{1}{S_{xx}}\sum(x_i-\bar{x} )= 0\)

\(\star \sum a_i x_i = \sum\frac{(x_i - \bar{x})x_i}{S_{xx}}= \frac{1}{S_{xx}} \sum(x_i - \bar{x})(x_i - \bar{x} + \bar{x}) = \frac{1}{S_{xx}} \sum(x_i - \bar{x})^2 + \frac{\bar{x}}{S_{xx}} \sum(x_i - \bar{x}) = \frac{1}{S_{xx}} \sum(x_i - \bar{x})^2 = 1\)

\(Var(\hat{\beta_0})\)

\(=Var(\bar{y} - \bar{x}\sum a_i x_i)\)

\(=Var(\frac{y_i}{n} - \bar{x}\sum a_i y_i)\)

\(=\frac{\sigma^2}{n} - \bar{x}^2\sigma^2\sum a_i^2\)

\(= \frac{\sigma^2}{n} - \frac{\bar{x}^2\sigma^2}{S_{xx}}\)

\(= \sigma^2(\frac{1}{n} - \frac{\bar{x}^2}{S_{xx}})\)

\(\star \sum a_i^2 = \sum\frac{(x_i - \bar{x})^2}{S_{xx}^2} = \frac{1}{S_{xx}^2}\sum(x_i - \bar{x})^2 = \frac{1}{S_{xx}}\)