Ridge Regression

Machine learning basic
능형회귀
Author

GUEBINCHOI

Published

March 31, 2021

Lasso and Ridge

능형회귀

다중공선성이 \(\hat{\beta}\)에 대한 분산과 공분산을 모두 크게한다.

ref: Montgomery, D. C., Peck, E. A., & Vining, G. G. (2021). Introduction to linear regression analysis. John Wiley & Sons.

아래와 같이 2개의 regressor가 존재하는 모형을 생각하자.

\(y_i=\beta_0+\beta_1x_{i1}+\beta_2 x_{i2}+\epsilon_i, \quad \epsilon_i ~ \sim iid N(0,\sigma^2)\)

편의상 아래를 가정하자.

\(s_y^2=\sum_{i=1}^{n}(y_i-\bar{y})^2=1\)

\(s_1^2=\sum_{i=1}^{n}(x_{i1}-\bar{x}_1)^2=1\)

\(s_2^2=\sum_{i=1}^{n}(x_{i2}-\bar{x}_2)^2=1\)

최소제곱추정법으로 \(\hat{\beta}_1\), \(\hat{\beta}_2\)를 구하면 아래와 같다.

\(\hat{\beta_1}=\frac{r_{1y}-r_{12}r_{2y}}{1-r_{12}^2}\).

\(\hat{\beta_2}=\frac{r_{2y}-r_{12}r_{1y}}{1-r_{12}^2}\).

단,

\(r_{1y}=\frac{s_{1y}}{\sqrt{s_1^2s_y^2}}=s_{1y}\), \(\quad s_{1y}=\sum_{i=1}^{n}(y_i-\bar{y})(x_{i1}-\bar{x}_1)\)

\(r_{2y}=\frac{s_{2y}}{\sqrt{s_2^2s_y^2}}=s_{2y}\), \(\quad s_{2y}=\sum_{i=1}^{n}(y_i-\bar{y})(x_{i2}-\bar{x}_2)\)

\(r_{12}=\frac{s_{12}}{\sqrt{s_1^2s_2^2}}=s_{12}\). \(\quad s_{12}=\sum_{i=1}^{n}(x_{i1}-\bar{x}_1)(x_{i2}-\bar{x}_2)\)

(관찰1)

만약에 \(x_1\)과 \(x_2\)사이에 강한 선형관계가 있다면 \(r_{12}\approx 1\) or \(r_{12}\approx -1\)

\(\hat{\beta}_1\)의 분모 = \(1-r_{12}^2 \approx 0\)

\(\hat{\beta}_1\)의 분자 \(\approx 0\)

\(\to\) \(\hat{\beta}_1\)와 \(\hat{\beta}_2\)의 값이 불안정할것 같다.

(관찰2)

\(\hat{\beta}_1\), \(\hat{\beta}_2\)의 분산과 공분산을 구해보자.

\(\mbox{V}(\hat{\beta_1})=\frac{1}{1-r_{12}^2}\sigma^2\)

\(\mbox{V}(\hat{\beta_2})=\frac{1}{1-r_{12}^2}\sigma^2\)

\(\mbox{cov}\big(\hat{\beta}_1,\hat{\beta}_2\big)=\frac{-r_{12}}{1-r_{12}^2}\sigma^2\)

(관찰3)

\(\mbox{cor}\big(\hat{\beta}_1,\hat{\beta}_2\big)=-r_{12}\)

import rpy2 
%load_ext rpy2.ipython
%%R 
set.seed(999)
n<-20000
toeic<-750+rnorm(n,sd=80)
toeic[toeic>990]<-990
toeic<-round(toeic)
teps<-toeic + rnorm(n,sd=0.01)
gpa<-3.5+rnorm(n,sd=0.3)
gpa[gpa>4.5]<-4.5 
gpa<-round(gpa,1)
sal<-gpa*600+toeic*5+rnorm(n,sd=300)
sal<-round(sal)
%%R 
cor(toeic,teps)
[1] 1

(직관)

토익이나 텝스점수나 그게 그거이다. (강한 상관관계)

원래모형은 연봉=학점*600+토익*5+오차인데, 토익이나 텝스나 그게 그거이므로, 아래와 같은 모형들도 거의 참모형이라고 생각할 수 있다.

  1. 연봉=학점*600+토익*2+텝스*3+오차

  2. 연봉=학점*600+토익*1+텝스*4+오차

  3. 연봉=학점*600+토익*(-5)+텝스*10+오차

  4. 연봉=학점*600+토익*(-1000)+텝스*(1005)+오차

  5. 연봉=학점*600+토익*(-10000)+텝스*(10005)+오차

…

결국에는 토익의 계수와 텝스의 계수를 더해서 5만되면 참모형

%%R 
lm1<-lm(sal~toeic+teps+gpa)
lm1

Call:
lm(formula = sal ~ toeic + teps + gpa)

Coefficients:
(Intercept)        toeic         teps          gpa  
      50.38       194.70      -189.72       590.53

토익의 계수는 194.70, 텝스의 계수는 -189.72 로 추정되었다. 두개더하면 대략 5.

몇번 더 시도를 해보자.

(시도2)

%%R 
set.seed(1)
n<-20000
toeic<-750+rnorm(n,sd=80)
toeic[toeic>990]<-990
toeic<-round(toeic)
teps<-toeic + rnorm(n,sd=0.01)
gpa<-3.5+rnorm(n,sd=0.3)
gpa[gpa>4.5]<-4.5 
gpa<-round(gpa,1)
sal<-gpa*600+toeic*5+rnorm(n,sd=300)
sal<-round(sal)
%%R 
lm1<-lm(sal~toeic+teps+gpa)
lm1

Call:
lm(formula = sal ~ toeic + teps + gpa)

Coefficients:
(Intercept)        toeic         teps          gpa  
     -45.82       -64.47        69.50       606.31

이번에는 토익의 계수는 -64.49, 텝스의 계수는 69.50 두개 더하면 대충 5

(시도3)

%%R 
set.seed(2)
n<-20000
toeic<-750+rnorm(n,sd=80)
toeic[toeic>990]<-990
toeic<-round(toeic)
teps<-toeic + rnorm(n,sd=0.01)
gpa<-3.5+rnorm(n,sd=0.3)
gpa[gpa>4.5]<-4.5 
gpa<-round(gpa,1)
sal<-gpa*600+toeic*5+rnorm(n,sd=300)
sal<-round(sal)
%%R 
lm1<-lm(sal~toeic+teps+gpa)
lm1

Call:
lm(formula = sal ~ toeic + teps + gpa)

Coefficients:
(Intercept)        toeic         teps          gpa  
      19.54       217.27      -212.31       603.10

토익의 계수는 217.27, 텝스의 계수는 -212.31 두개더하면 대충 5

(시도4)

%%R 
set.seed(3)
n<-20000
toeic<-750+rnorm(n,sd=80)
toeic[toeic>990]<-990
toeic<-round(toeic)
teps<-toeic + rnorm(n,sd=0.01)
gpa<-3.5+rnorm(n,sd=0.3)
gpa[gpa>4.5]<-4.5 
gpa<-round(gpa,1)
sal<-gpa*600+toeic*5+rnorm(n,sd=300)
sal<-round(sal)
%%R 
lm1<-lm(sal~toeic+teps+gpa)
lm1

Call:
lm(formula = sal ~ toeic + teps + gpa)

Coefficients:
(Intercept)        toeic         teps          gpa  
     -32.02      -152.82       157.85       600.85

토익의 계수는 -152.82, 텝스의 계수는 157.85 두개더하면 대충 5.

[다중공선성의 특징]

  1. 추정하는 \(\hat{\beta_1}\), \(\hat{\beta_2}\)가 어떤값일지 거의 예측안된다.
  • 5근처의 값이 나올때도 있고, 30근처의 값이 나오기도 하고, 100근처의 값이 나오기도 한다.
  • \(\hat{\beta}_1\), \(\hat{\beta}_2\)의 분산이 크다.
  1. 그래도 \(\hat{\beta}_1+\hat{\beta}_2\approx 5\)라는 공통점은 있음.

수식적으로 그럴듯해 보여도, 모두 바람직한 모형은 아니다.

아래는 모두 참모형이라고 생각되어지는 상황이다.

  1. \(\hat{\beta}_1=2\), \(\hat{\beta}_2=3\)

  2. \(\hat{\beta}_1=5\), \(\hat{\beta}_2=0\)

  3. \(\hat{\beta}_1=10\), \(\hat{\beta}_2=-5\)

모두 참모형에 가깝지만 상식적으로 (3)은 용납할 수 잆음.

이유1: (3)번과 같은 형태를 허용하면 \(\hat{\beta}_1=10000, ~ \hat{\beta}_2=-9995\) 와 같은식으로도 만들수 있음.

이유2: (해석불가능한 모델)

\(\hat{\beta}_2\)가 의미하는 것은 텝스점수가 얼마나 연봉에 영향을 주는지이다.

즉 텝스점수 1점을 올리면 연봉이 5만원 깍임.

상식적으로 말이 안된다.

해결책

논의를 간단하게 하기 위해서 모형을 좀 더 단순화 하자.

gpa에 대응하는 계수 600을 우리가 이미 알고있다고 가정하자. (혹은 적절하게 추정했다고 가정하자.)

그리고 오로지 연봉을 토익과 텝스만으로 추정한다고 하자.

단순화된 모형은

sal-600*gpa = toeic * β1 + teps * β2

이제 아래와 같이 계수를 추정하였을 경우

  1. \(\hat{\beta}_1=2\), \(\hat{\beta}_2=3\)

  2. \(\hat{\beta}_1=5\), \(\hat{\beta}_2=0\)

  3. \(\hat{\beta}_1=10\), \(\hat{\beta}_2=-5\)

(3)과 같은 상황이 발생하지 않도록 하여보자.

%%R 
set.seed(2)
n<-20000
toeic<-750+rnorm(n,sd=80)
toeic[toeic>990]<-990
toeic<-round(toeic)
teps<-toeic + rnorm(n,sd=0.01)
gpa<-3.5+rnorm(n,sd=0.3)
gpa[gpa>4.5]<-4.5 
gpa<-round(gpa,1)
sal<-gpa*600+toeic*5+rnorm(n,sd=300)
sal<-round(sal)
%%R
y<-sal-600*gpa
lm(y~toeic+teps-1)

Call:
lm(formula = y ~ toeic + teps - 1)

Coefficients:
 toeic    teps  
 216.9  -211.9

\(\hat{\beta}_1=216.9\)

\(\hat{\beta}_2=-211.9\)

위의 결과는 \(L(\beta)\)를 최소화하는 \(\beta\)를 구한 결과임

%%R 
X<-cbind(toeic,teps)
L<-function(beta){
    t(y-X%*%beta)%*%(y-X%*%beta)
}
%%R
beta<-c(216.9,-211.9)
c<-L(beta)

즉 \(c=1798374986\)이 \(L\)이 가질수 있는 최소값.

%%R
beta1<-c(2,3)
L1<-L(beta1)/c
beta2<-c(5,0)
L2<-L(beta2)/c
beta3<-c(10,-5)
L3<-L(beta3)/c
beta4<-c(104,-100)
L4<-L(beta4)/c
c(L1,L2,L3,L4)
[1] 1.000052 1.000050 1.000048 7.321030

  1. \(\hat{\beta}_1=2\), \(\hat{\beta}_2=3\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.000052\)

  2. \(\hat{\beta}_1=5\), \(\hat{\beta}_2=0\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.000050\)

  3. \(\hat{\beta}_1=10\), \(\hat{\beta}_2=-5\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.000048\)

  4. \(\hat{\beta}_1=104\), \(\hat{\beta}_2=-100\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=7.321030\)

이대로라면 위의 (1)-(4) 중에서 가장 적절한 해는 (3)이다.

아이디어: \(L(\beta)\)을 조금 바꾸자. 위의 손실함수에서 각각 \(\frac{1}{100000}\big(\beta_1^2+\beta_2^2\big)\)를 더한다면?

%%R
beta1<-c(2,3)
beta2<-c(5,0)
beta3<-c(10,-5)
beta4<-c(104,-100)
p1<-(beta1[1]^2+beta1[2]^2)/100000
p2<-(beta2[1]^2+beta2[2]^2)/100000
p3<-(beta3[1]^2+beta3[2]^2)/100000
p4<-(beta4[1]^2+beta4[2]^2)/100000

L1<-L(beta1)/c+p1
L2<-L(beta2)/c+p2
L3<-L(beta3)/c+p3
L4<-L(beta4)/c+p4
c(L1,L2,L3,L4)
[1] 1.000182 1.000300 1.001298 7.529190

  1. \(\hat{\beta}_1=2\), \(\hat{\beta}_2=3\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.000182\)

  2. \(\hat{\beta}_1=5\), \(\hat{\beta}_2=0\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.000300\)

  3. \(\hat{\beta}_1=10\), \(\hat{\beta}_2=-5\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=1.001298\)

  4. \(\hat{\beta}_1=104\), \(\hat{\beta}_2=-100\) \(\longrightarrow\) \(L(\boldsymbol{\beta})=7.529190\)

이렇게하면 이제 (수정된) \(L\)을 최소화하는 해는 (1)이다.

해결책의 시각적 이해

%%R
β1 = seq(-10,15,length=50)
β2 = seq(-10,15,length=50)
L_ <- function(β1,β2){
    rtn<-c()
    for(k in 1:length(β2)){
        rtn[k]<-sum((y-β1[k]*toeic-β2[k]*teps)^2)/c
    }
    rtn
}
z_=outer(β1,β2,L_)
#install.packages("plot3D")
library(plot3D) 
ribbon3D(z=z_,contour=TRUE,xlab="β1",ylab="β2",zlab="L(β1,β2)",main="original loss function")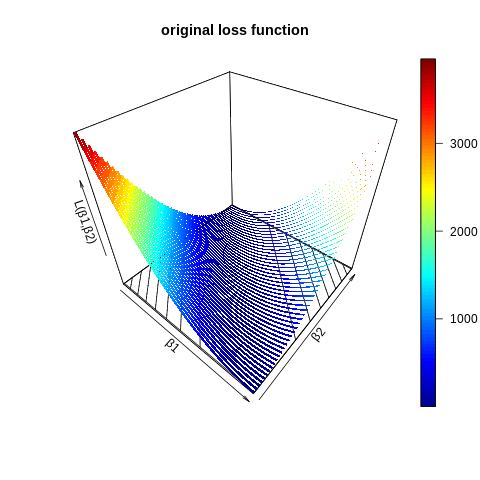

%%R
β1 = seq(-10,15,length=50)
β2 = seq(-10,15,length=50)
panelty_<-function(β1,β2){
    λ<-1.5 # 1/100000
    rtn<-c()
    for(k in 1:length(β2)){
        rtn[k]<-λ*sum(β1[k]^2+β2[k]^2)
    }
    rtn    
}

L_ <- function(β1,β2){
    rtn<-c()
    for(k in 1:length(β2)){
        rtn[k]<-sum((y-β1[k]*toeic-β2[k]*teps)^2)/c
    }
    rtn
}
z_=outer(β1,β2,L_)
z__=outer(β1,β2,panelty_)
#install.packages("plot3D")
library(plot3D) 
ribbon3D(z=z_,contour=TRUE,xlab="β1",ylab="β2",main="그림1: L(β1,β2)")
ribbon3D(z=z__,contour=TRUE,xlab="β1",ylab="β2",main="그림2: λ(β1^2+β2^2)")
ribbon3D(z=z_+z__,contour=TRUE,xlab="β1",ylab="β2",main="그림3: L(β1,β2)+λ(β1^2+β2^2)")

\(\lambda\)의 역할 \((\lambda>0)\)

[그림1]이랑 [그림2]을 섞어서 [그림3]을 만드는데, 각각을 얼만큼의 비율로 섞을지 결정한다.

람다가 크면 그림2를 많이 반영한다. \(\to\) 람다가 너무 크면 결국 \(\hat{\beta}_1\)와 \(\hat{\beta}_2\)의 추정값이 거의 0에 가깝게 된다.

람다가 작으면 그림1을 많이 반영한다. \(\to\) 람다가 너무 작게되면, 우리는 손실함수 \(L(\beta_1,\beta_2)\)에 아무런 수정도 하지않은 셈이된다.

\(\lambda(\beta_1^2+\beta_2^2)\)의 역할

원래 \(\beta_1+\beta_2=5\)를 만족하는 어떠한 해도 솔루션이 되었음. 즉 [그림1]과 같은 상황

[그림1]과 같은 상황에서 약간의 경사를 주어서 [그림3]과 같은 상황을 만듬

\(\hat{\beta}_1\) 와 \(\hat{\beta}_2\) 의 값을 안정적으로 만들어 준다.

그러면서도 딱히 원래 \(L(\beta_1,\beta_2)\)의 모양을 크게 해치지 않는다.

(!) 그럴듯함. 우리가 원하는것 같다.

이렇게 하면 다중공선성이 발생하는 상황에서 적절한 해를 구할 수 있을 것 같다.

(관찰)

\(\lambda\big(\beta_1^2+\beta_2^2\big)\)은 아래와 같이 표현가능함.

\(\lambda [\beta_1,\beta_2]\begin{bmatrix}\beta_1 \\ \beta_2 \end{bmatrix}=\lambda\beta^\top \beta\)

단, \(\beta=\begin{bmatrix}\beta_1 \\ \beta_2 \end{bmatrix}\).

릿지에 대한 책의 설명들..

Step 1. \(\hat{\beta}^R=\bf\big(X^\top X+\lambda I \big)^{-1}{\bf X}^\top y\).

일반적인 회귀분석과 다르게 아래와 같은 손실함수를 생각하자.

\(L={\bf (y-X\beta)^\top}{\bf (y-X\beta)}+\lambda \beta^\top \beta=\mbox{goodness of fit} + \mbox{panalty}\)

\(L\)를 최소화하는 \(\hat{\beta}\)을 구하면 아래와 같다. 구분을 위해서 \(\hat{\beta}^R\)이라는 기호를쓰자.

\(\hat{\beta}^R=\bf\big(X^\top X+\lambda I \big)^{-1}{\bf X}^\top y\)

Step 2 : \(\hat{\beta}^R\)이 \(\hat{\beta}^{OLS}\)보다 왜 좋은가?

\(\hat{\beta}^{OLS}={\bf (X^\top X)^{-1}X^\top y}\)

\(\hat{\beta}^{R}={\bf (X^\top X+\lambda I)^{-1}X^\top y}\)

  1. \(\hat{\beta}^{OLS}\)는 \(\beta\)에 대한 불편추정량 이지만, \(\hat{\beta}^{R}\)은 아니다.

  2. 하지만 분산은 \(\hat{\beta}^{OLS}\)보다 \(\hat{\beta}^R\)이 더 작다.

  3. 좋은 추정량은 bias와 분산이 모두 작아야하는데, \(\hat{\beta}^{R}\)은 바이어스는 \(\hat{\beta}^{OLS}\)보다 큰 상황이고, 분산은 \(\hat{\beta}^{OLS}\)보다 작은 상황이다.

  4. 따라서 두 추정치중에서 뭐가 더 좋다고 말하기 애매한데, 이를 명확하게 말하기 위해서는 MSE(\(=\mbox{bias}^2 + \mbox{variance}\))를 비교해봐야한다.

  5. Hoerl 과 Kennard는 \(\hat{\beta}^{R}\)이 \(\hat{\beta}^{OLS}\)보다 MSE가 작게되는 \(\lambda\)값이 항상 존재한다고 한다고 밝혔다. (1970년)

  6. 따라서 이러한 \(\lambda\)를 잘 찾으면 항상 Ridge Regression이 Linear Regression 보다 좋다고 주장할 수 있다.

(참고)

  1. 일반적인 손실함수 \(L={\bf (y-X\beta)^\top (y-X\beta)}\)와 수정된 손실함수를 구분하기 위해서 아래와 같이 \(\tilde{L}\)와 같은 기호를 쓰기도 한다.

\(\tilde{L}={\bf(y-X\beta)^\top(y-X\beta)+\lambda \beta^\top \beta }\)

  1. 일반적인 손실함수 \(L\)을 최소화하는 \(\beta\)와 수정된 손실함수 \(\tilde{L}\)을 최소화하는 \(\beta\)를 구분하기 위해서 아래와 같은 기호를 쓰기도 한다.

\(\hat{\beta}^{OLS}={\bf (X^\top X)^{-1}X^\top y}\)

\(\hat{\beta}^{R}={\bf (X^\top X+\lambda I)^{-1}X^\top y}\)

  1. \(\lambda \beta^\top \beta\)를 패널티항(=벌점항), \(L_2\)-패널티, regularization term (정규화항) 이라고 부른다.

  2. \(\lambda \beta^\top \beta\)를 \(\lambda \|\beta\|_2^2\)로 표현하기도 한다. \(\| \cdot \|_2\)는 벡터의 \(L_2\)-노름 이라고 한다.

  • \({\bf x}=(x_1,x_2)\) \(\to\) \(\|{\bf x}\|_2^2:=x_1^2+x_2^2\), \(\|{\bf x}\|_2:=\sqrt{x_1^2+x_2^2}\)
  • \(\lambda \beta^\top \beta = \lambda(\beta_1^2+\beta_2^2)\)

  1. (4)에서 유리하여 \(\lambda \beta^\top \beta\)를 \(L_2\)-패널티항이라고 부르기도 한다.

  2. 참고로 \(L_1\)-패널티항도 있다. 그리고 \(L_1\)과 \(L_2\)패널티를 섞어서 쓰는 방법도 있다.

  • \(Loss=SSE+L_2\mbox{-}panalty\): Ridge
  • \(Loss=SSE+L_1\mbox{-}panalty\): Lasso
  • \(Loss=SSE+L_1\mbox{-}panalty+L_2\mbox{-}panalty\): Elastic-net

  1. \(L_2\)-패널티항은 너무 큰 \(\beta_1,\beta_2\)를 구할때 패널티를 부여하여 되도록이면 작은 \(\beta_1,\beta_2\)을 선택하게끔 제약을 건다.

  2. 일반적인 손실함수 \(L\)이지만 우리는 \(\tilde{L}\)을 최소화해야 하므로 (i) 되도록이면 \(\beta_1,\beta_2\)의 값이 작을수록 좋다는 제약하에서 (ii) \(L\)를 최소화하는 2가지 역할을 수행해야 한다.

  3. \(\tilde{L}\)를 최소화하는 문제를 제약된 조건하에서의 최소화문제라고 표현한다.

  4. (8)에서 (i)-(ii)의 역할중에서 어떤것을 더 중시할지 조율하는 역할을 \(\lambda\)가 하는데, 이와 같은 이유로 \(\lambda\)를 조율모수 (tuning parameter)라고 부르기도 한다.

  5. \(\lambda\)를 하이퍼파라메터라고 부르기도 한다.

  6. \(\hat{\beta}^{R}\)의 값은 대체적으로 \(\hat{\beta}^{OLS}\)보다 작은값을 가진다. 이러한 이유로 \(\beta^{R}\) shrinkage esitmator라고 부른다.

  7. biased regression, shrinkage method, regularization method, panalty method.. 등 ridge를 표현하는 방법들은 다양하다.

  8. 능형회귀를 수행함에 있어서 (이론적인 부분에서는 언급되지 않았으나) 변수의 표준화를 먼저 시행해야 한다.